Structural Engineering – Design Example
Reinforced Concrete Column Design
Complete Step-by-Step Solution
Problem Statement
Design a reinforced concrete column for a 4-story office building. The column is located on the ground floor and must support loads from the upper floors. Determine the required longitudinal steel reinforcement.
Material Properties and Design Parameters
| Property | Value | Description |
|---|---|---|
| Concrete Class | C30 | Characteristic compressive strength: 30 MPa |
| Steel Class | S420 | Yield strength: 420 MPa |
| fcd | 20.0 MPa | Design concrete strength = 30/1.5 |
| fyd | 365 MPa | Design steel strength = 420/1.15 |
| fck | 30 MPa | Characteristic concrete strength |
Column Geometry and Loading
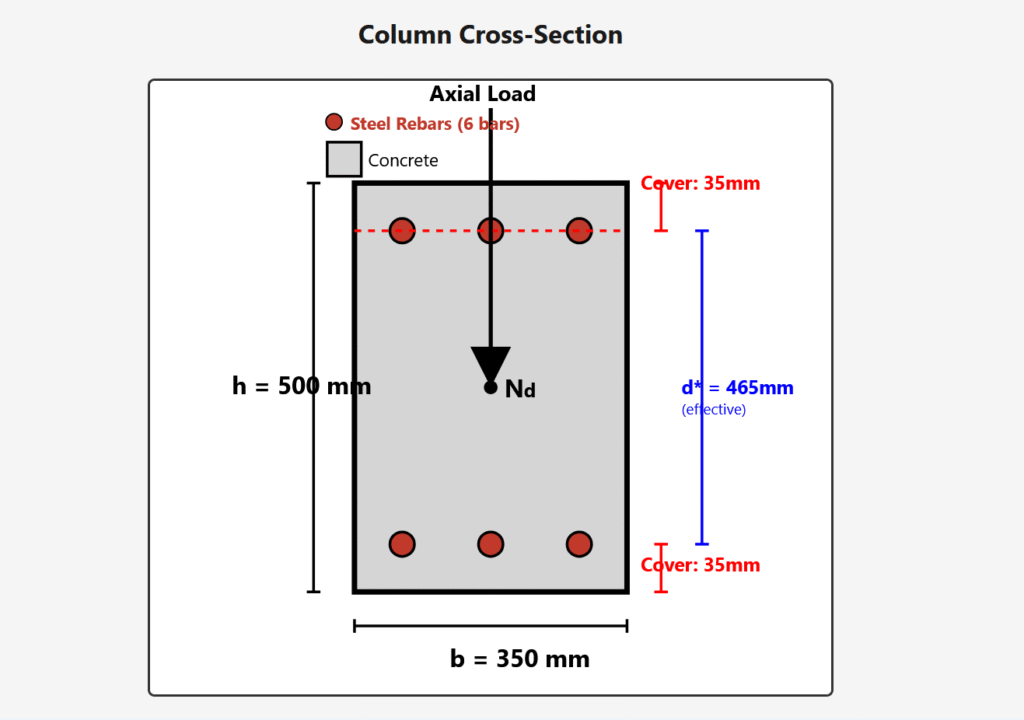
Column Cross-Section
Column Specifications:
- Width (b): 350 mm
- Height (h): 500 mm
- Cover: 35 mm on all sides
- Effective depth (d*): 500 – 35 = 465 mm
- Configuration: 6 steel reinforcement bars (shown as red circles)
Design Loading Conditions
The column must be designed for the following factored load combination:
| Load Type | Axial Force (Nd) | Bending Moment (Md) |
|---|---|---|
| Design Load | 950 kN | 140 kNm |
Note: These are ultimate limit state design loads including partial safety factors.
DESIGN SOLUTION – Step by Step Calculation
Step 1
Check Adequacy of Column Dimensions
Check: Nd ≤ Ndm = 0.5 × Ac × fck
Where:
Ac = b × h = 350 × 500 = 175,000 mm²
fck = 30 MPa
Ndm = 0.5 × 175,000 × 30 = 2,625,000 N = 2,625 kN
Nd = 950 kN ≤ 2,625 kN ✓
Where:
Ac = b × h = 350 × 500 = 175,000 mm²
fck = 30 MPa
Ndm = 0.5 × 175,000 × 30 = 2,625,000 N = 2,625 kN
Nd = 950 kN ≤ 2,625 kN ✓
Result: Column dimensions are adequate! Applied load (950 kN) is only 36% of maximum capacity (2,625 kN). This provides excellent safety margin.
What does this mean?
We have verified that the concrete cross-section is sufficiently large to carry the axial load. The 0.5 factor ensures we don’t rely on 100% of concrete capacity for conservative design. Since 950 < 2,625, we can proceed with these dimensions.
We have verified that the concrete cross-section is sufficiently large to carry the axial load. The 0.5 factor ensures we don’t rely on 100% of concrete capacity for conservative design. Since 950 < 2,625, we can proceed with these dimensions.
Step 2
Calculate Effective Depth Ratio
d*/h = 465/500 = 0.93
Significance:
This dimensionless ratio (0.93) indicates the relative position of reinforcement within the section. It’s used for reading interaction diagrams and design charts. A value of 0.93 means the steel centroid is positioned at 93% of the section depth from the top.
This dimensionless ratio (0.93) indicates the relative position of reinforcement within the section. It’s used for reading interaction diagrams and design charts. A value of 0.93 means the steel centroid is positioned at 93% of the section depth from the top.
Step 3
Calculate Normalized Axial Load
ν = Nd / (b × h × fcd)
ν = 950,000 / (350 × 500 × 20.0)
ν = 950,000 / 3,500,000
ν = 0.271 ≈ 0.27
ν = 950,000 / (350 × 500 × 20.0)
ν = 950,000 / 3,500,000
ν = 0.271 ≈ 0.27
Physical Meaning:
The normalized axial force (ν = 0.27) represents the proportion of concrete design capacity being utilized. At 27%, this is a moderately loaded column. This dimensionless parameter enables use of standardized interaction diagrams.
The normalized axial force (ν = 0.27) represents the proportion of concrete design capacity being utilized. At 27%, this is a moderately loaded column. This dimensionless parameter enables use of standardized interaction diagrams.
Step 4
Calculate Load Eccentricity
e = Md / Nd
e = 140 × 10⁶ / 950 × 10³
e = 147.4 mm ≈ 147 mm
e = 140 × 10⁶ / 950 × 10³
e = 147.4 mm ≈ 147 mm
Check minimum eccentricity:
emin = 15 + 0.003h = 15 + 0.003(500) = 15 + 1.5 = 16.5 mm
Our e = 147 mm > 16.5 mm ✓
emin = 15 + 0.003h = 15 + 0.003(500) = 15 + 1.5 = 16.5 mm
Our e = 147 mm > 16.5 mm ✓
Understanding Eccentricity:
Eccentricity (e = 147 mm) represents the perpendicular distance from the column centerline to the line of action of the axial load. This is 42% of the column width (147/350 = 0.42), indicating significant bending moment must be considered in the design.
Eccentricity (e = 147 mm) represents the perpendicular distance from the column centerline to the line of action of the axial load. This is 42% of the column width (147/350 = 0.42), indicating significant bending moment must be considered in the design.
Step 5
Calculate Normalized Bending Moment
μ = Md / (b × h² × fcd)
μ = 140 × 10⁶ / (350 × 500² × 20.0)
μ = 140 × 10⁶ / 1,750,000,000
μ = 0.080
μ = 140 × 10⁶ / (350 × 500² × 20.0)
μ = 140 × 10⁶ / 1,750,000,000
μ = 0.080
Interpretation:
The normalized moment (μ = 0.080) represents the bending moment as a fraction of the section’s moment capacity. This moderate value indicates the column experiences both significant compression and bending.
The normalized moment (μ = 0.080) represents the bending moment as a fraction of the section’s moment capacity. This moderate value indicates the column experiences both significant compression and bending.
Step 6
Determine Steel Coefficient (ψ) from Design Charts
Using interaction diagram with:
– ν = 0.27 (normalized axial force)
– μ = 0.080 (normalized moment)
– d*/h = 0.93
Result: ψ ≈ 0.10
– ν = 0.27 (normalized axial force)
– μ = 0.080 (normalized moment)
– d*/h = 0.93
Result: ψ ≈ 0.10
About ψ:
The steel coefficient (ψ = 0.10) is obtained from column interaction diagrams that account for the combined compression-bending behavior. This coefficient directly relates to the required steel reinforcement ratio.
The steel coefficient (ψ = 0.10) is obtained from column interaction diagrams that account for the combined compression-bending behavior. This coefficient directly relates to the required steel reinforcement ratio.
Step 7
Calculate Required Steel Ratio
ρs = ψ × (fcd / fyd)
ρs = 0.10 × (20.0 / 365)
ρs = 0.10 × 0.0548
ρs = 0.00548 = 0.548%
ρs = 0.10 × (20.0 / 365)
ρs = 0.10 × 0.0548
ρs = 0.00548 = 0.548%
Compare with minimum requirement:
ρmin = 1.0% (per design code)
ρs,calculated = 0.548% < ρmin
Decision: Must use ρmin = 1.0%
ρmin = 1.0% (per design code)
ρs,calculated = 0.548% < ρmin
Decision: Must use ρmin = 1.0%
Why minimum steel requirement?
Although calculation shows 0.548% is sufficient, codes mandate minimum 1% steel to ensure:
Although calculation shows 0.548% is sufficient, codes mandate minimum 1% steel to ensure:
- Adequate structural ductility and warning before failure
- Control of concrete shrinkage and thermal cracks
- Sufficient reserve capacity for unforeseen loads
- Proper structural behavior under seismic conditions
Step 8
Calculate Total Required Steel Area
Ast = ρs × b × h
Ast = 0.01 × 350 × 500
Ast = 1,750 mm²
Ast = 0.01 × 350 × 500
Ast = 1,750 mm²
Design Requirement:
We need a total cross-sectional area of 1,750 mm² of steel reinforcement. This will be distributed as longitudinal bars around the column perimeter. Next step is to select appropriate bar sizes and quantities.
We need a total cross-sectional area of 1,750 mm² of steel reinforcement. This will be distributed as longitudinal bars around the column perimeter. Next step is to select appropriate bar sizes and quantities.
Step 9
Select Bar Size and Number
Try n = 6 bars (suitable for rectangular columns)
Required area per bar = Ast / n = 1,750 / 6 = 291.7 mm²
For circular bar: A = πز/4
Solving for Ø:
Ø = √(4A/π) = √(4 × 291.7 / π) = √(371.5) = 19.3 mm
Required area per bar = Ast / n = 1,750 / 6 = 291.7 mm²
For circular bar: A = πز/4
Solving for Ø:
Ø = √(4A/π) = √(4 × 291.7 / π) = √(371.5) = 19.3 mm
Standard Bar Sizes:
Available diameters: …, 16, 18, 20, 22, 25, 28, 32, …mm
Required: 19.3 mm → Round UP to: Ø20 mm
Critical Rule: Always round up to ensure adequate steel area is provided!
Available diameters: …, 16, 18, 20, 22, 25, 28, 32, …mm
Required: 19.3 mm → Round UP to: Ø20 mm
Critical Rule: Always round up to ensure adequate steel area is provided!
Step 10
Verify Final Design
Selected design: 6Ø20
Area of Ø20 bar = π × 20²/4 = 314 mm²
Total area provided = 6 × 314 = 1,884 mm²
Required area = 1,750 mm²
Check: 1,884 > 1,750 ✓
Area of Ø20 bar = π × 20²/4 = 314 mm²
Total area provided = 6 × 314 = 1,884 mm²
Required area = 1,750 mm²
Check: 1,884 > 1,750 ✓
FINAL DESIGN: 6Ø20
(Six bars of 20mm diameter)
(Six bars of 20mm diameter)
Design is satisfactory!
- Provided steel area: 1,884 mm²
- Required steel area: 1,750 mm²
- Excess: 134 mm² (7.7% over – acceptable)
- Steel ratio provided: 1,884/(350×500) = 1.08% > 1.0% minimum ✓
Design Summary
| Parameter | Value | Status |
|---|---|---|
| Column dimensions | 350 mm × 500 mm | Adequate ✓ |
| Design axial force | 950 kN | Within capacity ✓ |
| Design bending moment | 140 kNm | Within capacity ✓ |
| Required steel area | 1,750 mm² | Provided: 1,884 mm² ✓ |
| Steel ratio | ρmin = 1.0% | Provided: 1.08% ✓ |
| Final reinforcement | 6Ø20 | Acceptable ✓ |
Additional Design Considerations
Bar Spacing Requirements:
- Minimum clear spacing between bars: 25 mm (greater of bar diameter or 25mm)
- With 6 bars of Ø20 in a 350×500 column: adequate spacing is achieved ✓
- Clear spacing = (350 – 2×35 – 3×20)/2 = 110 mm >> 25 mm ✓
Transverse Reinforcement (Ties/Links):
- Minimum tie diameter: Ø8 mm (at least 1/4 of longitudinal bar diameter)
- Maximum spacing: 300 mm or 15 times longitudinal bar diameter
- Recommended design: Ø10 @ 200 mm spacing
Concrete Cover Requirements:
- Specified cover: 35 mm (measured to outermost steel, including ties)
- Provides adequate durability protection and fire resistance
- Suitable for internal column in normal exposure conditions
Key Design Insights
- Lightly loaded column: Utilizing only 36% of concrete capacity (950 kN vs 2,625 kN maximum)
- Minimum steel controls: Calculated 0.548% but using 1.08% due to code minimum of 1.0%
- Significant eccentricity: 147 mm (42% of column width) indicates notable bending effects
- Efficient arrangement: 6 bars provide good distribution for rectangular section
- Adequate margins: All design checks passed with comfortable safety factors
Construction Specification
COLUMN: 350 × 500 mm
Longitudinal Reinforcement: 6Ø20
Ties: Ø10 @ 200 mm c/c
Concrete Grade: C30
Steel Grade: S420
Concrete Cover: 35 mm
