Reinforced Concrete Design – Shear Reinforcement
Column Shear Reinforcement Design
Transverse Reinforcement for Confinement and Middle Zones – C25-S420
Example Problem
For a column with C25-S420 materials and cross-section (300/500) mm, subjected to an axial load Nd = 540 kN and shear force Vd = 350 kN, calculate the transverse reinforcement (stirrup) spacing for confinement and middle zones according to normal ductility requirements.
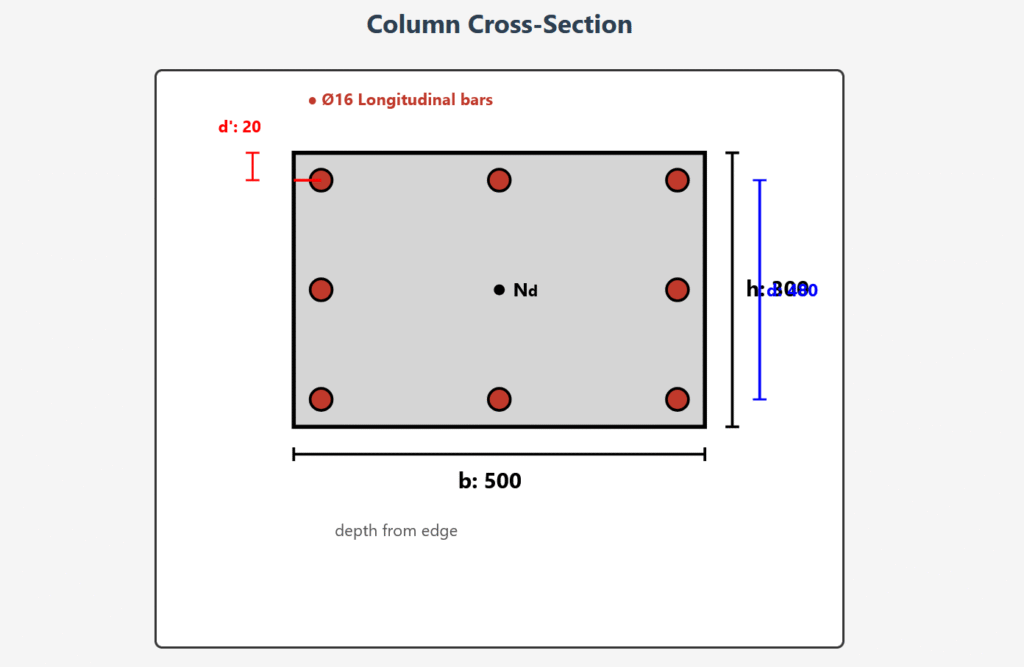
Given: Longitudinal reinforcement diameter Ø16, Stirrup diameter Ø8
Column Cross-Section
Given Information
| Parameter | Value |
|---|---|
| Column dimensions | b = 500 mm, h = 300 mm |
| Materials | C25-S420 (fcd = 16.67 MPa ≈ 17 MPa, fyd = 365 MPa, fctd = 1.15 MPa) |
| Design axial force | Nd = 540 kN |
| Design shear force | Vd = 350 kN |
| Longitudinal reinforcement | Ø16 bars |
| Stirrup diameter | Ø8 |
| Effective depth | d = 480 mm (from calculation) |
| Ductility level | Normal |
SOLUTION – Shear Reinforcement Design
Step 1
Check Maximum Shear Force Capacity
Vd ≤ 0.22 Ac fcd
350 × 10³ ≤ 0.22 × 300 × 500 × 17
350 × 10³ ≤ 561 × 10³ N
350 < 561 kN ✓
350 × 10³ ≤ 0.22 × 300 × 500 × 17
350 × 10³ ≤ 561 × 10³ N
350 < 561 kN ✓
Result: Section is adequate for shear (adequate in section, column section shear strength is satisfied).
Step 2
Calculate Concrete Shear Contribution
Vd ≤ Vcr
Vcr = 0.65 fctd b d (1 + 0.07 Nd/Ac)
Vcr = 0.65 × 1.15 × 300 × 480 (1 + 0.07 × 540×10³/(300×500))
Vcr = 0.65 × 1.15 × 300 × 480 (1 + 0.07 × 3.6)
Vcr = 107,640 (1 + 0.252)
Vcr = 107,640 × 1.252 = 134,765.3 N ≈ 134.765 kN
Vcr = 0.65 fctd b d (1 + 0.07 Nd/Ac)
Vcr = 0.65 × 1.15 × 300 × 480 (1 + 0.07 × 540×10³/(300×500))
Vcr = 0.65 × 1.15 × 300 × 480 (1 + 0.07 × 3.6)
Vcr = 107,640 (1 + 0.252)
Vcr = 107,640 × 1.252 = 134,765.3 N ≈ 134.765 kN
Note: The axial load increases the concrete’s shear resistance through the [1 + 0.07(Nd/Ac)] factor. Here it provides a 25.2% increase.
Since Vd = 350 kN > Vcr = 134.765 kN, shear reinforcement is required.
Stirrup area (two-legged Ø8):
Asw = n × (πز/4) = 2 × (π × 8²/4)
Asw = 2 × 50.27 = 100.48 mm²
Asw = n × (πز/4) = 2 × (π × 8²/4)
Asw = 2 × 50.27 = 100.48 mm²
Step 3
Calculate Required Stirrup Contribution
Concrete contribution (normal ductility):
Vc = 0.8 Vcr
Vc = 0.8 × 134.765 = 107.812 kN
Vc = 0.8 × 134.765 = 107.812 kN
Required stirrup contribution:
Vs = Vd – Vc
Vs = 350 – 107.812 = 242.2 kN
Vs = 350 – 107.812 = 242.2 kN
CONFINEMENT ZONE (Sarılma Bölgesi)
Step 4
Calculate Stirrup Spacing from Shear Requirements
s = (Asw × fywd × d) / Vs
s = (100.48 × 365 × 480) / (242.2 × 10³)
s = 17,604,096 / 242,200
s = 72.68 mm
s = (100.48 × 365 × 480) / (242.2 × 10³)
s = 17,604,096 / 242,200
s = 72.68 mm
Step 5
Apply Maximum Spacing Limits for Confinement Zone
Maximum Spacing Requirements:
sc ≤ min {
b/3 = 300/3 = 100 mm
8Ølong = 8 × 16 = 128 mm
150 mm
}
Therefore: sc ≤ 100 mm
Selected sc = 75 mm
b/3 = 300/3 = 100 mm
8Ølong = 8 × 16 = 128 mm
150 mm
}
Therefore: sc ≤ 100 mm
Selected sc = 75 mm
Decision: Although calculations give 72.68 mm, we select practical value of 75 mm (divisible by 5).
Step 6
Check Minimum Reinforcement Requirement – Confinement Zone
Asw/sc ≥ 0.3 (fcd/fywd) b (minimum condition)
100.48/75 ≥ 0.3 × (17/365) × 300
1.34 ≥ 0.3 × 0.0466 × 300
1.34 > 0.28 ✓
100.48/75 ≥ 0.3 × (17/365) × 300
1.34 ≥ 0.3 × 0.0466 × 300
1.34 > 0.28 ✓
Confinement zone design: Ø8 @ 75 mm
MIDDLE REGION (Orta Bölge)
Step 7
Apply Maximum Spacing Limits for Middle Region
Maximum Spacing Requirements:
so ≤ min {
b/2 = 300/2 = 150 mm
12Ølong = 12 × 16 = 192 mm
200 mm
}
Therefore: so ≤ 150 mm
Selected so = 150 mm
b/2 = 300/2 = 150 mm
12Ølong = 12 × 16 = 192 mm
200 mm
}
Therefore: so ≤ 150 mm
Selected so = 150 mm
Step 8
Check Minimum Reinforcement Requirement – Middle Region
Asw/so ≥ 0.3 (fcd/fywd) b (minimum condition)
100.48/150 ≥ 0.3 × (17/365) × 300
0.67 ≥ 0.28
0.67 > 0.28 ✓
100.48/150 ≥ 0.3 × (17/365) × 300
0.67 ≥ 0.28
0.67 > 0.28 ✓
Middle region design: Ø8 @ 150 mm
Design Summary
Final Stirrup Arrangement
| Parameter | Value | Status |
|---|---|---|
| Maximum shear capacity check | 350 kN < 561 kN | ✓ Adequate |
| Concrete cracking force (Vcr) | 134.765 kN | With axial load effect |
| Concrete contribution (Vc) | 107.812 kN | = 0.8 Vcr |
| Required stirrup contribution (Vs) | 242.2 kN | = Vd – Vc |
| Stirrup area (Asw) | 100.48 mm² | Two-legged Ø8 |
| Calculated spacing from shear | 72.68 mm | Base calculation |
| Confinement zone spacing | sc = 75 mm | ✓ Final (Ø8/75) |
| Confinement zone – Min. requirement | 1.34 > 0.28 | ✓ Satisfied |
| Middle region spacing | so = 150 mm | ✓ Final (Ø8/150) |
| Middle region – Min. requirement | 0.67 > 0.28 | ✓ Satisfied |
Key Design Insights
- Two different zones: Confinement zones (near beam-column joints) require tighter stirrup spacing (75mm) than middle region (150mm).
- Axial load benefit: The 540 kN axial load increases concrete shear capacity by 25.2% through the [1 + 0.07(Nd/Ac)] factor.
- Shear governs spacing: Calculated spacing from shear (72.68 mm) is more critical than code maximum limits (100 mm for confinement zone).
- Minimum reinforcement: Both zones satisfy the minimum Asw/s requirement (1.34 > 0.28 and 0.67 > 0.28).
- Practical spacing: Selected 75 mm and 150 mm are practical values divisible by 5 or 10 for construction ease.
- Zone lengths: Confinement zones extend approximately 80-100mm from each end (max(b/3, 8Ølong, 150mm)).
Final Construction Specifications
COLUMN: 300 mm × 500 mm
Longitudinal Reinforcement: Ø16 bars
Confinement Zone Stirrups: Ø8 @ 75 mm
Middle Region Stirrups: Ø8 @ 150 mm
Materials: C25 Concrete, S420 Steel
Stirrup Type: Two-legged rectangular ties
Ductility Level: Normal
⚠️ Important Construction Notes:
- Confinement zones (sarılma bölgesi) are critical areas requiring tighter stirrup spacing for enhanced ductility.
- Stirrup hooks must be 135° with minimum 6d extension (where d = stirrup diameter).
- Maintain consistent stirrup spacing within each zone – no irregular spacing allowed.
- All designs must comply with local building codes and be reviewed by a licensed engineer.
- Consider seismic detailing requirements if the structure is in a seismic zone.
