Reinforced Concrete Design – Spiral Column
Spiral Column Design
Longitudinal Reinforcement and Spiral Spacing – C20-S420
Example Problem
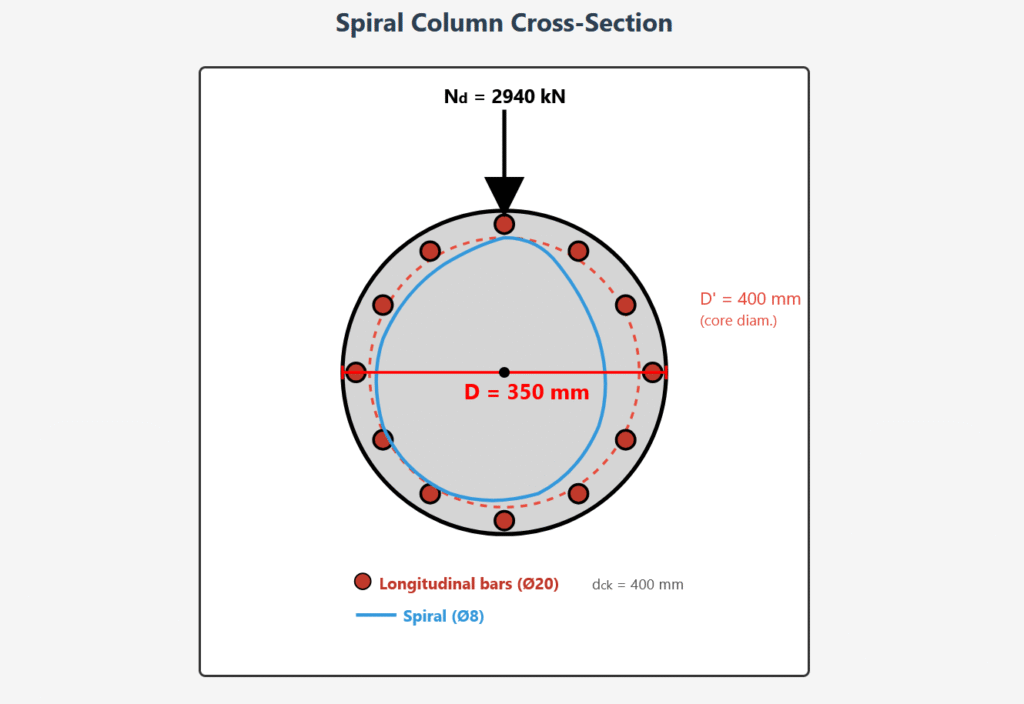
For a spiral column shown in the figure, made of C20-S420 materials, subjected to an axial load Nd = 2940 kN:
a) Calculate the required longitudinal reinforcement area using Ø20 diameter bars.
b) Calculate the spiral spacing using Ø8 spiral reinforcement.
Spiral Column Cross-Section
Given Information
| Parameter | Value |
|---|---|
| Column type | Circular spiral column (Fretli kolon) |
| Diameter | D = 350 mm |
| Core diameter | D’ = 400 mm (outer diameter), dck = 400 mm |
| Materials | C20-S420 (fcd = 13.3 MPa, fyd = 365 MPa) |
| Design axial force | Nd = 2940 kN |
| Longitudinal bar diameter | Ø20 mm |
| Spiral bar diameter | Ø8 mm |
PART A: LONGITUDINAL REINFORCEMENT CALCULATION
Step 1
Calculate Column Areas
Gross concrete area:
Ac = π d²/4 = π × 400²/4 = 125,600 mm²
Core area (inside spiral):
Ack = π D’²/4 = π × 350²/4 = 96,163 mm²
Ac = π d²/4 = π × 400²/4 = 125,600 mm²
Core area (inside spiral):
Ack = π D’²/4 = π × 350²/4 = 96,163 mm²
Note: Ac is the total column area, while Ack is the confined core area within the spiral reinforcement.
Step 2
Calculate Required Steel Area Using Basic Equation
Nd = 0.85 fcd Ac + fyd Ast
2940 × 10³ = 0.85 × 13 × 125,600 + 365 Ast
2940 × 10³ = 1,387,960 + 365 Ast
365 Ast = 2,940,000 – 1,387,960
365 Ast = 1,552,040
Ast = 4252.4 mm²
2940 × 10³ = 0.85 × 13 × 125,600 + 365 Ast
2940 × 10³ = 1,387,960 + 365 Ast
365 Ast = 2,940,000 – 1,387,960
365 Ast = 1,552,040
Ast = 4252.4 mm²
Formula explanation:
– 0.85 fcd Ac: Concrete contribution to axial capacity
– fyd Ast: Steel contribution to axial capacity
– 0.85 fcd Ac: Concrete contribution to axial capacity
– fyd Ast: Steel contribution to axial capacity
Step 3
Determine Number of Longitudinal Bars
Given: Use Ø20 bars
Area of one Ø20 bar = π × 20²/4 = 314 mm²
Required number of bars:
n = Ast / (area per bar)
n = 4252.4 / 314 = 13.5 → Round up to 14 bars
Area of one Ø20 bar = π × 20²/4 = 314 mm²
Required number of bars:
n = Ast / (area per bar)
n = 4252.4 / 314 = 13.5 → Round up to 14 bars
Selected design: 14Ø20
Verification:
Provided area: 14 × 314 = 4,396 mm²
Required area: 4,252.4 mm²
4,396 > 4,252.4 ✓
Provided area: 14 × 314 = 4,396 mm²
Required area: 4,252.4 mm²
4,396 > 4,252.4 ✓
PART B: SPIRAL SPACING CALCULATION
Step 4
Check Section Adequacy for Spiral Columns
Nd > 0.20 Ac fck
2940 × 10³ > 0.20 × 125,600 × 20
2940 × 10³ > 502,400 N
2,940,000 > 502,400 ✓
2940 × 10³ > 0.20 × 125,600 × 20
2940 × 10³ > 502,400 N
2,940,000 > 502,400 ✓
Result: Since Nd > 0.20 Ac fck, spiral reinforcement is required!
Step 5
Calculate Required Volumetric Spiral Ratio (ρst)
Spiral Ratio Formula (Two conditions – select larger):
Condition 1:
ρst ≥ 0.45 [(Ac/Ack) – 1] × (fck/fywk)
Condition 2:
ρst ≥ 0.12 × (fck/fywk)
ρst ≥ 0.45 [(Ac/Ack) – 1] × (fck/fywk)
Condition 2:
ρst ≥ 0.12 × (fck/fywk)
Calculate Condition 1:
ρst ≥ 0.45 [(125,600/96,163) – 1] × (20/365)
ρst ≥ 0.45 × [1.306 – 1] × 0.0548
ρst ≥ 0.45 × 0.306 × 0.0548
ρst ≥ 0.0075
ρst ≥ 0.45 × [1.306 – 1] × 0.0548
ρst ≥ 0.45 × 0.306 × 0.0548
ρst ≥ 0.0075
Calculate Condition 2:
ρst ≥ 0.12 × (20/365)
ρst ≥ 0.12 × 0.0548
ρst ≥ 0.00657
ρst ≥ 0.12 × 0.0548
ρst ≥ 0.00657
Select larger value: ρst = 0.0075
Step 6
Calculate Required Spiral Area per Unit Height
Ast = ρst × Ack
Ast = 0.0075 × 96,163 = 721.22 mm²
Ast = 0.0075 × 96,163 = 721.22 mm²
What is Ast?
This is the required spiral steel area per unit height of column. It represents how much spiral reinforcement cross-sectional area is needed per mm of column height.
This is the required spiral steel area per unit height of column. It represents how much spiral reinforcement cross-sectional area is needed per mm of column height.
Step 7
Calculate Spiral Spacing
st = (π D Aswt) / Ast
Where:
D = core diameter = 350 mm
Aswt = area of spiral bar = π × Ø²/4 = π × 8²/4 = 50.24 mm²
Ast = required area per unit height = 721.22 mm²
st = (3.14 × 350 × 50.24) / 721.22
st = 55,234.48 / 721.22
st = 76.55 mm → Round to 77 mm
Where:
D = core diameter = 350 mm
Aswt = area of spiral bar = π × Ø²/4 = π × 8²/4 = 50.24 mm²
Ast = required area per unit height = 721.22 mm²
st = (3.14 × 350 × 50.24) / 721.22
st = 55,234.48 / 721.22
st = 76.55 mm → Round to 77 mm
Step 8
Apply Code Limits for Spiral Spacing
Maximum Spacing Limits:
st ≤ min {
D/5 = 350/5 = 70 mm
80 mm
}
Therefore: st ≤ 70 mm
D/5 = 350/5 = 70 mm
80 mm
}
Therefore: st ≤ 70 mm
Check: Calculated spacing = 77 mm > 70 mm limit
Decision: Must use maximum allowed spacing: st = 70 mm
Decision: Must use maximum allowed spacing: st = 70 mm
Final spiral design: Ø8 / 70 mm (Ø8 spiral at 70mm spacing)
Design Summary
Final Spiral Column Design
| LONGITUDINAL REINFORCEMENT | ||
|---|---|---|
| Parameter | Value | Status |
| Column diameter | D = 350 mm | Given |
| Gross area (Ac) | 125,600 mm² | Calculated |
| Core area (Ack) | 96,163 mm² | Calculated |
| Required steel area | 4,252.4 mm² | From equilibrium |
| Final longitudinal design | 14Ø20 | 4,396 mm² ✓ |
| SPIRAL REINFORCEMENT | ||
|---|---|---|
| Parameter | Value | Status |
| Adequacy check | 2,940 kN > 502.4 kN | ✓ Spiral required |
| Volumetric ratio – Condition 1 | ρst ≥ 0.0075 | Calculated |
| Volumetric ratio – Condition 2 | ρst ≥ 0.00657 | Calculated |
| Selected volumetric ratio | ρst = 0.0075 | Larger value selected |
| Required area per unit height | Ast = 721.22 mm² | Calculated |
| Calculated spacing | 76.55 mm → 77 mm | From formula |
| Maximum allowed spacing | 70 mm (D/5) | Code limit |
| Final spiral design | Ø8 / 70 mm | ✓ Code compliant |
Key Design Insights
- Spiral vs. Tied columns: Spiral columns provide better confinement and ductility compared to tied columns due to continuous spiral reinforcement.
- High axial load: Nd = 2,940 kN greatly exceeds 0.20Acfck = 502.4 kN, confirming the need for spiral reinforcement.
- Two spiral ratio conditions: Code requires checking both formulas and using the larger value (0.0075 vs. 0.00657).
- Code limits govern: Calculated spacing (77 mm) exceeds maximum allowed (70 mm), so code limit controls the design.
- Core diameter: The confined core diameter (D’ = 350 mm) is measured to the centerline of the spiral.
- Longitudinal bars: 14Ø20 bars are distributed evenly around the column perimeter for balanced reinforcement.
- Construction: Spiral must be continuous (no splices) or spliced with proper lap length per code requirements.
Advantages of Spiral Columns
- Superior confinement: Continuous spiral provides better concrete confinement than discrete ties
- Enhanced ductility: Confined concrete exhibits more ductile behavior under compression
- Higher strength: Confinement increases effective concrete strength
- Better performance: Particularly beneficial in seismic regions
- Uniform reinforcement: No weak zones as with tied columns
Final Construction Specifications
SPIRAL COLUMN: Ø400 mm (Outer diameter)
Core Diameter: 350 mm (to centerline of spiral)
Longitudinal Reinforcement: 14Ø20
(14 bars of 20mm diameter, equally spaced around perimeter)
Spiral Reinforcement: Ø8 @ 70 mm pitch
(Continuous spiral, 8mm diameter, 70mm vertical spacing)
Materials: C20 Concrete, S420 Steel
Cover: 25-30 mm to spiral
⚠️ Important Construction Notes:
- Spiral reinforcement must be continuous or properly lap-spliced (minimum 48db lap length)
- Maintain accurate spiral spacing throughout column height – use spacers if needed
- Longitudinal bars must be positioned accurately around the perimeter (angular spacing = 360°/14 ≈ 25.7°)
- Ensure adequate concrete cover to spiral (25-30mm minimum)
- Spiral must be anchored properly at top and bottom with 1.5 extra turns
- All designs must be reviewed by a licensed structural engineer
- Follow local building codes for specific requirements in your region
