Structural Engineering – Biaxial Column Design
Square RC Column with Double Ties
Biaxial Bending & Shear Reinforcement Design
Problem Statement
Design a square reinforced concrete column subjected to combined axial load, biaxial bending moment, and shear force. Determine:
a) Column adequacy and required longitudinal reinforcement
b) Double tie configuration and spacing for Ø8 mm stirrups
Material Properties
| Property | Value | Description |
|---|---|---|
| Concrete Class | C20 | fck = 20 MPa |
| Steel Class | S420 | fyk = 420 MPa |
| fcd | 13.33 MPa | Design concrete strength (20/1.5) |
| fyd | 365 MPa | Design steel strength (420/1.15) |
| fctd | 1.0 MPa | Design tensile strength |
| Cover | d’ = 30 mm | Concrete cover to reinforcement |
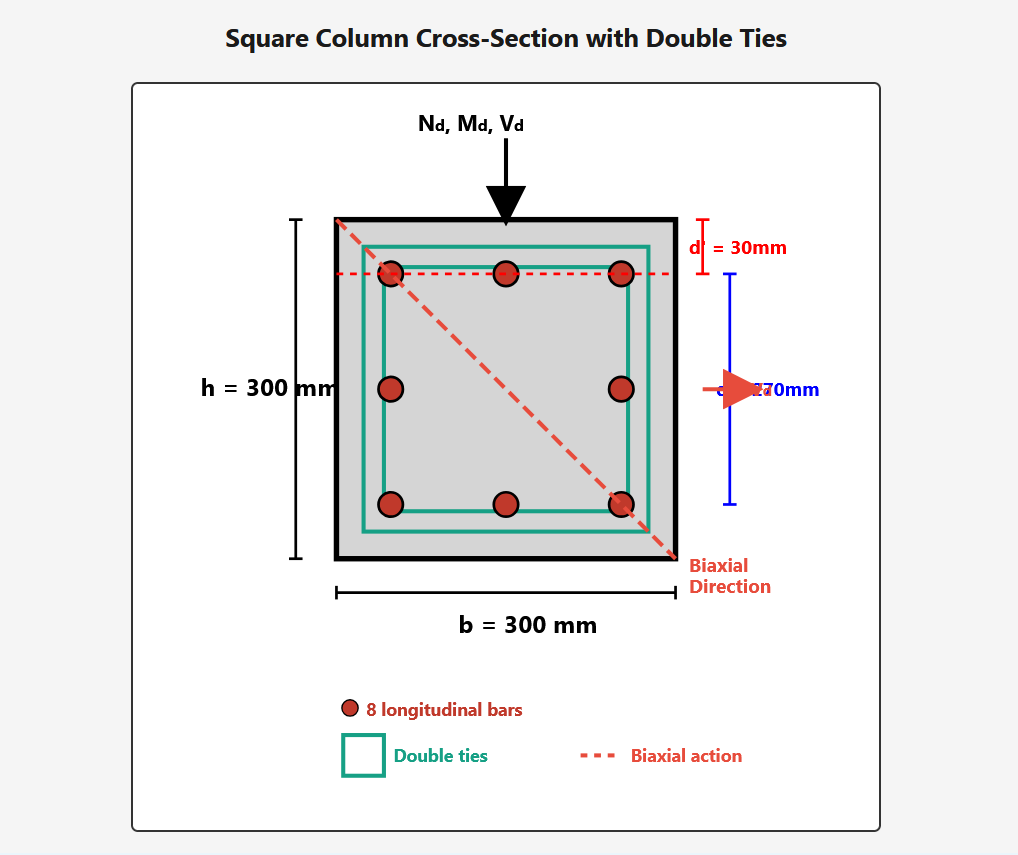
Column Geometry and Loading
Square Column Cross-Section with Double Ties
Column Specifications:
- Width (b): 300 mm
- Height (h): 300 mm (square section)
- Cover (d’): 30 mm
- Effective depth (d): 300 – 30 = 270 mm
- Reinforcement: 8 corner & intermediate bars + double ties
- Loading: Biaxial bending with shear
Design Loading Conditions
| Load Type | Value |
|---|---|
| Axial Force (Nd) | 235 kN |
| Bending Moment (Md) | 96.53 kNm |
| Shear Force (Vd) | 240 kN |
Note: These are factored ultimate limit state loads including biaxial effects.
PART A: LONGITUDINAL REINFORCEMENT DESIGN
Step 1
Check Column Dimensions Adequacy
Nd ≤ Ndm = 0.5 × Ac × fck
Where:
Ac = b × h = 300 × 300 = 90,000 mm²
fck = 20 MPa
Ndm = 0.5 × 90,000 × 20 = 900,000 N = 900 kN
Nd = 235 kN ≤ 900 kN ✓
Where:
Ac = b × h = 300 × 300 = 90,000 mm²
fck = 20 MPa
Ndm = 0.5 × 90,000 × 20 = 900,000 N = 900 kN
Nd = 235 kN ≤ 900 kN ✓
Result: Column dimensions are adequate! Applied load (235 kN) is only 26% of maximum capacity (900 kN).
Step 2
Calculate Effective Depth Ratio
d”/h = (h – d’)/h = (300 – 30)/300 = 270/300
d”/h = 0.9
Or as given in notation: d”/h = 240/300 = 0.8 (to center of reinforcement)
d”/h = 0.9
Or as given in notation: d”/h = 240/300 = 0.8 (to center of reinforcement)
Effective depth: This ratio is used to read interaction diagrams for biaxially loaded square columns.
Step 3
Calculate Normalized Axial Force
ν = Nd / (b × h × fcd)
ν = 235,000 / (300 × 300 × 13.33)
ν = 235,000 / 1,199,700
ν = 0.196 ≈ 0.20
ν = 235,000 / (300 × 300 × 13.33)
ν = 235,000 / 1,199,700
ν = 0.196 ≈ 0.20
Normalized axial force: At ν = 0.20, this represents low to moderate axial compression, where bending effects are significant.
Step 4
Calculate Normalized Bending Moment
μ = Md / (b × h² × fcd)
μ = 96.53 × 10⁶ / (300 × 300² × 13.33)
μ = 96,530,000 / 359,910,000
μ = 0.268 ≈ 0.27
μ = 96.53 × 10⁶ / (300 × 300² × 13.33)
μ = 96,530,000 / 359,910,000
μ = 0.268 ≈ 0.27
Normalized moment: μ = 0.27 indicates significant bending moment relative to section capacity. This is a moment-dominated design case.
Step 5
Determine Steel Coefficient from Interaction Diagram
From biaxial column interaction diagram:
With ν = 0.20 and μ = 0.27
Read: ψ ≈ 0.60
With ν = 0.20 and μ = 0.27
Read: ψ ≈ 0.60
High steel coefficient: ψ = 0.60 is relatively high, indicating substantial reinforcement is needed due to the large bending moment with moderate axial load.
Step 6
Calculate Required Steel Ratio
ρs = ψ × (fcd / fyd)
ρs = 0.60 × (13.33 / 365)
ρs = 0.60 × 0.0365
ρs = 0.0219 ≈ 0.021 = 2.1%
ρs = 0.60 × (13.33 / 365)
ρs = 0.60 × 0.0365
ρs = 0.0219 ≈ 0.021 = 2.1%
Check against code limits:
ρmin = 1.0%, ρmax = 4.0%
ρs = 2.1% is within limits ✓
ρmin = 1.0%, ρmax = 4.0%
ρs = 2.1% is within limits ✓
Step 7
Calculate Total Required Steel Area
Ast = ρs × b × h
Ast = 0.021 × 300 × 300
Ast = 1,890 mm²
Ast = 0.021 × 300 × 300
Ast = 1,890 mm²
Step 8
Select Bar Size and Number
Try n = 8 bars (typical for square column with double ties)
Required area per bar = Ast / n = 1,890 / 8 = 236.25 mm²
For circular bar: A = πز/4
Ø = √(4A/π) = √(4 × 236.25 / π) = √(300.2) = 17.33 mm
Round up to standard size: Ø18 mm
Verification:
Area of Ø18 = π × 18²/4 = 254 mm²
Total provided = 8 × 254 = 2,032 mm²
2,032 mm² > 1,890 mm² ✓
Required area per bar = Ast / n = 1,890 / 8 = 236.25 mm²
For circular bar: A = πز/4
Ø = √(4A/π) = √(4 × 236.25 / π) = √(300.2) = 17.33 mm
Round up to standard size: Ø18 mm
Verification:
Area of Ø18 = π × 18²/4 = 254 mm²
Total provided = 8 × 254 = 2,032 mm²
2,032 mm² > 1,890 mm² ✓
ANSWER (Part a):
Longitudinal Reinforcement: 8Ø18
Steel ratio provided: 2,032/(300×300) = 2.26% ✓
Longitudinal Reinforcement: 8Ø18
Steel ratio provided: 2,032/(300×300) = 2.26% ✓
PART B: SHEAR REINFORCEMENT DESIGN (DOUBLE TIES)
Step 9
Calculate Concrete Shear Capacity
Check if shear reinforcement is required:
Vd ≤ 0.22 × Asw × fcd
For preliminary check:
240,000 N ≤ (0.22 × 300 × 13.33) = 879.8 N/mm × h
This is a minimum check; detailed capacity calculation needed.
Vd ≤ 0.22 × Asw × fcd
For preliminary check:
240,000 N ≤ (0.22 × 300 × 13.33) = 879.8 N/mm × h
This is a minimum check; detailed capacity calculation needed.
Step 10
Calculate Effective Depth for Shear
d = h – d’ = 300 – 30 = 270 mm
Step 11
Calculate Concrete Shear Resistance
Vcr = 0.65 × fctd × b × d × (1 + 0.07 × Nd/Ac)
Where fctd = 1.0 MPa (for C20)
Vcr = 0.65 × 1.0 × 300 × 270 × (1 + 0.07 × 235,000/90,000)
Vcr = 52,650 × (1 + 0.07 × 2.611)
Vcr = 52,650 × (1 + 0.183)
Vcr = 52,650 × 1.183
Vcr = 62,285 N ≈ 62.3 kN
Where fctd = 1.0 MPa (for C20)
Vcr = 0.65 × 1.0 × 300 × 270 × (1 + 0.07 × 235,000/90,000)
Vcr = 52,650 × (1 + 0.07 × 2.611)
Vcr = 52,650 × (1 + 0.183)
Vcr = 52,650 × 1.183
Vcr = 62,285 N ≈ 62.3 kN
Shear check:
Vd = 240 kN > Vcr = 62.3 kN
→ Shear reinforcement is required!
Vd = 240 kN > Vcr = 62.3 kN
→ Shear reinforcement is required!
Step 12
Calculate Required Stirrup Area
For double ties (4 legs effective in shear per section):
Using Ø8 ties: Asw1 = π × 8²/4 = 50.24 mm²
Total stirrup area for 4 legs:
Asw = 4 × 50.24 = 200.96 mm²
Using Ø8 ties: Asw1 = π × 8²/4 = 50.24 mm²
Total stirrup area for 4 legs:
Asw = 4 × 50.24 = 200.96 mm²
Double ties: Two overlapping rectangular ties provide 4 vertical legs on each face, significantly improving shear resistance and confinement.
Step 13
Calculate Shear Carried by Concrete
Vc = 0.8 × Vcr
Vc = 0.8 × 62.3 = 49.8 kN
Shear to be carried by stirrups:
Vs = Vd – Vc
Vs = 240 – 49.8 = 190.2 kN
Vc = 0.8 × 62.3 = 49.8 kN
Shear to be carried by stirrups:
Vs = Vd – Vc
Vs = 240 – 49.8 = 190.2 kN
Step 14
Calculate Required Stirrup Spacing
From shear design equation:
s = (Asw × fyd × d) / Vs
s = (200.96 × 365 × 270) / 190,200
s = 19,794,552 / 190,200
s = 104.1 mm
s = (Asw × fyd × d) / Vs
s = (200.96 × 365 × 270) / 190,200
s = 19,794,552 / 190,200
s = 104.1 mm
Step 15
Check Maximum Spacing Limits
Code maximum spacing limits:
s ≤ b/3 = 300/3 = 100 mm
s ≤ 12Ømin = 12 × 18 = 216 mm
s ≤ 150 mm (general limit)
Calculated: s = 104 mm
Governing: s ≤ 100 mm (b/3 criterion)
s ≤ b/3 = 300/3 = 100 mm
s ≤ 12Ømin = 12 × 18 = 216 mm
s ≤ 150 mm (general limit)
Calculated: s = 104 mm
Governing: s ≤ 100 mm (b/3 criterion)
Spacing check: Calculated spacing (104 mm) is close to the b/3 limit (100 mm).
Step 16
Verify Minimum Shear Reinforcement
Check minimum reinforcement requirement:
(Asw/s) ≥ 0.3 × (fctd/fywd) × b
(200.96/100) ≥ 0.3 × (1.0/365) × 300
2.0096 ≥ 0.3 × 0.00274 × 300
2.0096 ≥ 0.247 ✓
(Asw/s) ≥ 0.3 × (fctd/fywd) × b
(200.96/100) ≥ 0.3 × (1.0/365) × 300
2.0096 ≥ 0.3 × 0.00274 × 300
2.0096 ≥ 0.247 ✓
Minimum reinforcement satisfied!
Step 17
Select Final Tie Spacing
Select standard spacing: s = 100 mm
(Meets both strength and maximum spacing requirements)
(Meets both strength and maximum spacing requirements)
ANSWER (Part b):
Double Tie Configuration: Ø8 @ 100 mm c/c
(Two overlapping rectangular ties at 100mm spacing)
Double Tie Configuration: Ø8 @ 100 mm c/c
(Two overlapping rectangular ties at 100mm spacing)
Complete Design Summary
| Design Parameter | Required | Provided | Status |
|---|---|---|---|
| Column dimensions | 300 × 300 mm | 300 × 300 mm | ✓ |
| Axial load | Nd = 235 kN | Capacity adequate | ✓ |
| Bending moment | Md = 96.53 kNm | Capacity adequate | ✓ |
| Shear force | Vd = 240 kN | Stirrups provided | ✓ |
| Normalized values | ν = 0.20, μ = 0.27 | From analysis | ✓ |
| Steel coefficient | ψ = 0.60 | From diagram | ✓ |
| Steel ratio | ρs = 2.1% | 2.26% | ✓ |
| Steel area | 1,890 mm² | 2,032 mm² | ✓ |
| Longitudinal steel | 8 bars | 8Ø18 | ✓ |
| Concrete shear | Vcr = 62.3 kN | Vc = 49.8 kN | ✓ |
| Steel shear | Vs = 190.2 kN | Provided by ties | ✓ |
| Stirrup spacing | s ≤ 100 mm | 100 mm | ✓ |
| Transverse steel | Double ties | Ø8 @ 100 mm | ✓ |
Double Tie Configuration Details
What are Double Ties?
- Two overlapping rectangular stirrups in the same section
- Each tie encloses different corner bars
- Provides 4 vertical legs on each face (2 from each tie)
- Superior confinement compared to single ties
- Better control of longitudinal bar buckling
Advantages for Biaxial Loading:
- Enhanced confinement in both directions
- Better distribution of shear resistance
- Improved ductility under biaxial bending
- All longitudinal bars are laterally supported
Design Verification:
- Tie diameter: Ø8 mm (adequate for Ø18 longitudinal bars) ✓
- Spacing: 100 mm (≤ b/3, ≤ 12Ø, ≤ 150mm) ✓
- Number of legs: 4 per section (excellent shear capacity) ✓
- Shear capacity: Vd = 240 kN < Vu (ultimate) ✓
Key Design Insights
- Biaxial loading: The diagonal orientation in the cross-section indicates biaxial bending effects considered in design
- Moment-dominated: High μ = 0.27 with moderate ν = 0.20 indicates bending controls design
- High reinforcement: Steel ratio of 2.26% is above minimum, driven by bending moment requirements
- Shear critical: Vd = 240 kN is much higher than concrete capacity (62.3 kN), requiring substantial stirrups
- Double tie advantage: 4 legs per section provide 200.96 mm² shear area, doubling single tie capacity
- Close spacing: 100mm spacing governed by b/3 requirement ensures excellent confinement
- Ductile design: Double ties enhance ductility, critical for columns under biaxial loading
- Practical construction: 8 bars with double ties provides symmetric arrangement for biaxial behavior
Construction Drawing Specification
SQUARE COLUMN: 300 × 300 mm
LONGITUDINAL REINFORCEMENT: 8Ø18
TRANSVERSE REINFORCEMENT: DOUBLE TIES Ø8 @ 100 mm c/c
TIE CONFIGURATION: Two overlapping rectangular stirrups
CONCRETE GRADE: C20 (fck = 20 MPa)
STEEL GRADE: S420 (fyk = 420 MPa)
CONCRETE COVER: 30 mm clear
TIE HOOKS: 135° with 10Ø extension, alternated at corners
DESIGN LOADS: Nd=235kN, Md=96.53kNm, Vd=240kN
