Structural Engineering – Worked Example
ROOF TRUSS DESIGN PROBLEM
Load Calculation and Joint Force Analysis
PROBLEM STATEMENT
Calculate the joint loads at the support points of a roof truss structure according to the given data:
- Truss Spacing: 5.5 m
- Structure Weight (Self-weight): 12 kg/m²
- Roof Covering Load: 18 kg/m²
- Altitude: 1400 m above sea level
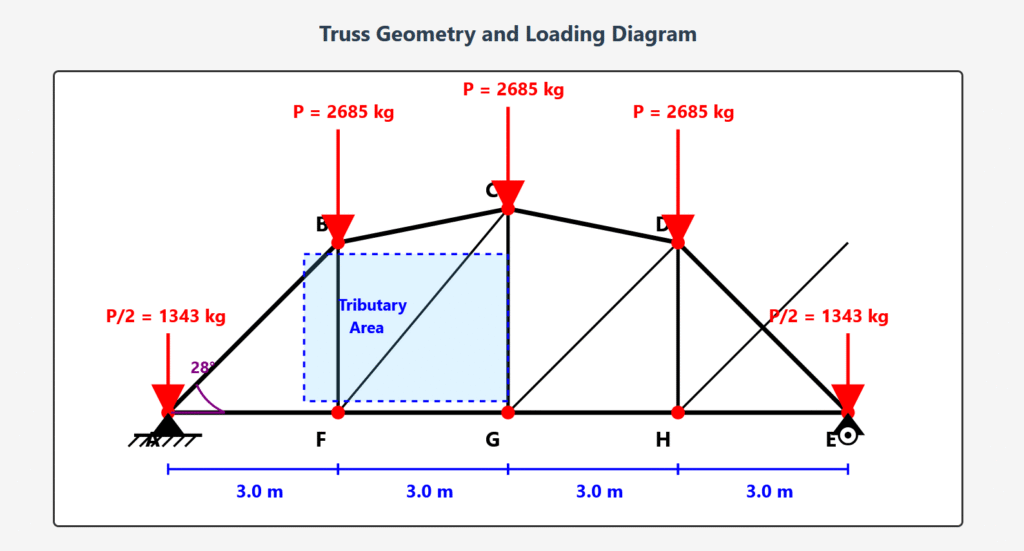
- Roof Slope Angle: 28°
- Total Span: 12 m (divided into 4 panels of 3 m each)
Truss Geometry and Loading Diagram
Given Data Summary
| Parameter | Symbol | Value |
|---|---|---|
| Truss Spacing | – | 5.5 m |
| Structure Self-weight | PMA | 12 kg/m² |
| Roof Covering Load | PÇÖ | 18 kg/m² |
| Altitude | H | 1400 m |
| Roof Slope Angle | α | 28° |
| Panel Width | – | 3.0 m |
| Total Span | L | 12 m |
SOLUTION – Step by Step Calculations
Step 1
Calculate Geometric Properties
First, find the sloped length (DE) using the bottom chord and angle:
Cos(28°) = horizontal distance / sloped length
Cos(28°) = 3.0 / DE
DE = 3.0 / Cos(28°)
DE = 3.0 / 0.8829
DE = 3.40 m
Cos(28°) = horizontal distance / sloped length
Cos(28°) = 3.0 / DE
DE = 3.0 / Cos(28°)
DE = 3.0 / 0.8829
DE = 3.40 m
Calculate the height (DH) using trigonometry:
tan(28°) = DH / 3.0
DH = 3.0 × tan(28°)
DH = 3.0 × 0.5317
DH = 1.60 m
tan(28°) = DH / 3.0
DH = 3.0 × tan(28°)
DH = 3.0 × 0.5317
DH = 1.60 m
Verification:
We can verify: DH / DE = sin(28°) → 1.60 / 3.40 = 0.47 ≈ 0.469 = sin(28°) ✓
We can verify: DH / DE = sin(28°) → 1.60 / 3.40 = 0.47 ≈ 0.469 = sin(28°) ✓
Step 2
Calculate Tributary Areas
S1 – Sloped Area (Tributary area on slope):
S1 = DE × Truss Spacing
S1 = 3.40 × 5.5
S1 = 18.70 m²
S1 = DE × Truss Spacing
S1 = 3.40 × 5.5
S1 = 18.70 m²
S2 – Horizontal Projection Area:
S2 = Panel width × Truss Spacing
S2 = 3.0 × 5.5
S2 = 16.50 m²
S2 = Panel width × Truss Spacing
S2 = 3.0 × 5.5
S2 = 16.50 m²
Understanding Tributary Areas:
- S1 (Sloped area) is used for loads that act perpendicular to the slope (roof covering, self-weight)
- S2 (Horizontal area) is used for loads that act vertically (snow, structure weight)
Step 3
Calculate Snow Load (Pk)
Snow load formula (altitude-dependent):
Pk = 75 + 0.08(H – 1000) kg/m²
For H = 1400 m:
Pk = 75 + 0.08(1400 – 1000)
Pk = 75 + 0.08(400)
Pk = 75 + 32
Pk = 107 kg/m²
Pk = 75 + 0.08(H – 1000) kg/m²
For H = 1400 m:
Pk = 75 + 0.08(1400 – 1000)
Pk = 75 + 0.08(400)
Pk = 75 + 32
Pk = 107 kg/m²
Snow Load Intensity: Pk = 107 kg/m²
Note: Snow load increases with altitude because higher elevations typically receive more snowfall. The formula accounts for this by adding 0.08 kg/m² for every meter above 1000m elevation.
Step 4
Calculate Total Snow Load at Joint (Wk)
Total snow load on one panel:
Wk = Pk × S2
Wk = 107 × 16.50
Wk = 1,766 kg
Wk = Pk × S2
Wk = 107 × 16.50
Wk = 1,766 kg
Snow Load at Each Interior Joint: Wk = 1,766 kg
This is the total snow load that acts on one panel. Since snow acts vertically downward, we use the horizontal projection area (S2).
Step 5
Calculate Wind Load (PR)
Wind load formula:
PR = 150 × (sin α)²
PR = 150 × (sin 28°)²
PR = 150 × (0.469)²
PR = 150 × 0.220
PR = 33.0 kg/m²
PR = 150 × (sin α)²
PR = 150 × (sin 28°)²
PR = 150 × (0.469)²
PR = 150 × 0.220
PR = 33.0 kg/m²
Wind Load Intensity: PR = 33.0 kg/m²
Understanding: Wind load is proportional to the square of sin(α), meaning steeper roofs experience greater wind loads due to increased surface area exposed to wind pressure.
Step 6
Calculate Total Wind Load at Joint (WR)
Total wind load on one panel:
WR = PR × S2
WR = 33.0 × 16.50
WR = 545 kg
WR = PR × S2
WR = 33.0 × 16.50
WR = 545 kg
Wind Load at Each Interior Joint: WR = 545 kg
Step 7
Calculate Roof Covering Load (WÇÖ)
Total roof covering load on one panel:
WÇÖ = PÇÖ × S1
WÇÖ = 18 × 18.70
WÇÖ = 337 kg
WÇÖ = PÇÖ × S1
WÇÖ = 18 × 18.70
WÇÖ = 337 kg
Roof Covering Load at Each Interior Joint: WÇÖ = 337 kg
Note: Roof covering load uses the sloped area (S1) because the roofing material is distributed along the actual slope of the roof.
Step 8
Calculate Structure Self-Weight (WMA)
Total self-weight on one panel:
WMA = PMA × S2
WMA = 12 × 16.50
WMA = 198 kg
WMA = PMA × S2
WMA = 12 × 16.50
WMA = 198 kg
Structure Self-Weight at Each Interior Joint: WMA = 198 kg
Note: Structure self-weight uses horizontal projection area (S2) as it represents the weight of the truss members acting vertically downward.
Step 9
Calculate Total Load at Interior Joints
Sum of all loads:
ΣP = Wk + WR + WÇÖ + WMA
ΣP = 1,766 + 545 + 337 + 198
ΣP = 2,846 kg
ΣP = Wk + WR + WÇÖ + WMA
ΣP = 1,766 + 545 + 337 + 198
ΣP = 2,846 kg
Total Load at Each Interior Joint (B, C, D): P = 2,846 kg ≈ 2,850 kg
Load Distribution Summary:
- Snow Load: 1,766 kg (62%)
- Wind Load: 545 kg (19%)
- Roof Covering: 337 kg (12%)
- Self-Weight: 198 kg (7%)
- Total: 2,846 kg (100%)
Step 10
Calculate Support Reactions
Total load from all joints:
4P = 4 × 2,846 = 11,384 kg
Due to symmetry:
Ay = Ey = 4P / 2
Ay = Ey = 11,384 / 2
Ay = Ey = 5,692 kg
4P = 4 × 2,846 = 11,384 kg
Due to symmetry:
Ay = Ey = 4P / 2
Ay = Ey = 11,384 / 2
Ay = Ey = 5,692 kg
Support Reactions: Ay = Ey = 5,692 kg ≈ 5,700 kg
Verification:
Check equilibrium: ΣFy = 0
Ay + Ey – 4P = 0
5,692 + 5,692 – 11,384 = 0 ✓
Check equilibrium: ΣFy = 0
Ay + Ey – 4P = 0
5,692 + 5,692 – 11,384 = 0 ✓
Step 11
Load Distribution at Support Joints
At support joints A and E, the load is half of interior joints:
P/2 = 2,846 / 2
P/2 = 1,423 kg ≈ 1,425 kg
P/2 = 2,846 / 2
P/2 = 1,423 kg ≈ 1,425 kg
Why half load at supports?
- Support joints (A and E) only receive load from one adjacent panel
- Interior joints (B, C, D) receive load from panels on both sides
- This is a standard assumption in truss analysis
Summary of Results
| Description | Symbol | Calculated Value |
|---|---|---|
| Sloped Length | DE | 3.40 m |
| Height | DH | 1.60 m |
| Sloped Tributary Area | S1 | 18.70 m² |
| Horizontal Tributary Area | S2 | 16.50 m² |
| Snow Load Intensity | Pk | 107 kg/m² |
| Wind Load Intensity | PR | 33 kg/m² |
| Total Snow Load | Wk | 1,766 kg |
| Total Wind Load | WR | 545 kg |
| Total Roof Covering Load | WÇÖ | 337 kg |
| Total Self-Weight | WMA | 198 kg |
| Load at Interior Joints (B, C, D) | P | 2,846 kg ≈ 2,850 kg |
| Load at Support Joints (A, E) | P/2 | 1,423 kg ≈ 1,425 kg |
| Support Reactions | Ay = Ey | 5,692 kg ≈ 5,700 kg |
FINAL ANSWER
Joint Loads:
Interior Joints (B, C, D): P = 2,850 kg
Support Joints (A, E): P/2 = 1,425 kg
Support Reactions:
Ay = Ey = 5,700 kg
Key Takeaways from This Problem
- Geometric calculations are essential before load calculations (finding sloped length, height)
- Two different tributary areas are used: sloped area for roof covering, horizontal area for vertical loads
- Snow load increases with altitude – each meter above 1000m adds 0.08 kg/m²
- Wind load depends on roof angle – steeper roofs have higher wind loads
- Load superposition – all loads are added together for total design load
- Support joints receive half the load of interior joints due to tributary area distribution
- Symmetry simplifies calculations – reactions at both supports are equal
Important Notes for Design:
- These loads represent unfactored service loads. For ultimate limit state design, apply appropriate load factors according to design codes (typically 1.2 for dead loads, 1.6 for live loads).
- The analysis assumes loads are applied only at joints, which is the fundamental assumption for truss analysis.
- This problem calculated loads for one specific load combination. In actual design, multiple load combinations must be checked.
