Isolated Spread Footing Design
Complete Step-by-Step Solution
Problem Statement
Design an isolated spread footing for a square column (700 × 700 mm) carrying an axial load. The footing must be designed considering soil bearing capacity, punching shear, one-way shear, and flexural requirements. Determine the footing dimensions, thickness, and reinforcement.
Given Design Data
| Parameter | Value |
|---|---|
| Column dimensions | b = l = 700 mm (square) |
| Axial load (Nd) | 2500 kN (factored) |
| Allowable soil pressure (σem) | 350 kN/m² |
| Concrete grade | C30 (fck = 30 MPa) |
| Steel grade | S420 (fyk = 420 MPa) |
| Design concrete strength | fcd = 20 MPa (30/1.5) |
| Design steel strength | fyd = 365 MPa (420/1.15) |
| Tensile strength | fctd = 1.0 MPa |
| Concrete cover | d’ = 50 mm |
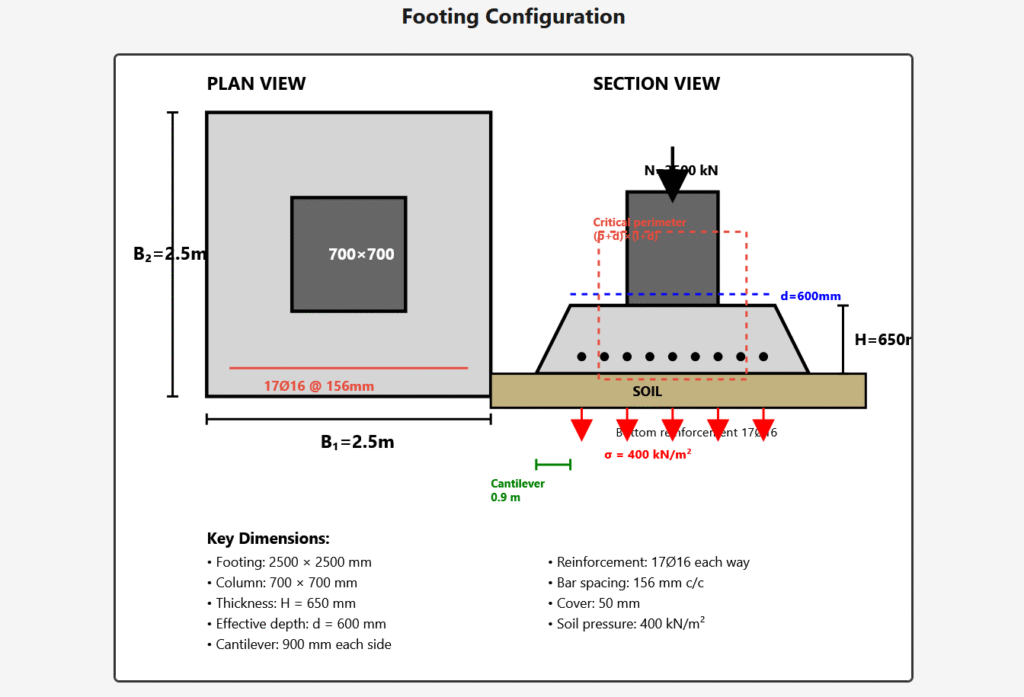
Footing Configuration
DESIGN SOLUTION
Determine Soil Bearing Capacity
σem = 350 kN/m²
Enhanced bearing capacity considering footing weight:
fzm = 1.5 × σem
fzm = 1.5 × 350 = 525 kN/m²
The factor 1.5 accounts for the improved bearing capacity under the footing weight and the factored load conditions. This is a simplified approach used in preliminary design.
Calculate Required Footing Area
fzm = Nd / (B₁ × B₂)
525 = 2500 / (B₁ × B₂)
(B₁ × B₂) = 2500 / 525 = 4.76 m²
For square footing: B₁ = B₂
B = √4.76 = 2.18 m
Select: B₁ = B₂ = 2.5 m (round up for safety)
Always round up to ensure adequate bearing area. Using 2.5 m provides a comfortable margin and uses standard dimensions for easier construction.
Calculate Actual Soil Pressure
σz = Nd / (B₁ × B₂)
σz = 2500 / (2.5 × 2.5)
σz = 2500 / 6.25
σz = 400 kN/m²
Soil bearing capacity is satisfied with good margin (24% reserve).
Initial Thickness Selection
Effective depth:
d = H – d’ = 450 – 50 = 400 mm
Verify modified bearing capacity:
fzm = fcd – 18H
fzm = 525 – (18 × 0.45)
fzm = 525 – 8.1
fzm = 516.9 ≈ 517 kN/m²
Bearing capacity remains adequate.
Punching Shear Check (First Trial: H = 450 mm)
b₁ = b + d = 0.7 + 0.4 = 1.1 m
b₂ = b + d = 0.7 + 0.4 = 1.1 m
Area within critical perimeter:
Ap = b₁ × b₂ = 1.1 × 1.1 = 1.21 m²
Critical perimeter length:
up = 2(b₁ + b₂) = 2(1.1 + 1.1) = 4.4 m
(γ = 1 for axial load only)
Punching shear force:
Vpd = Nd – σz × Ap
Vpd = 2500 – (400 × 1.21)
Vpd = 2500 – 484
Vpd = 2016 kN
Punching shear capacity:
Vpr = γ × fctd × up × d
Vpr = 1 × 1 × 4400 × 400
Vpr = 1,760,000 N = 1760 kN
Vpd = 2016 kN > Vpr = 1760 kN ✗
The footing thickness is INSUFFICIENT for punching shear!
Thickness must be increased.
Recalculate Required Thickness
Vpd = γ × fctd × up × d
2016 kN = (1 × 1 × 4400 × d) N
2,016,000 = 4400 × d
d = 2,016,000 / 4400
d = 458 mm ≈ 460 mm
Required total thickness:
H = d + d’ = 460 + 50 = 510 mm
Select conservatively: H = 650 mm
Effective depth: d = 600 mm
We select H = 650 mm (rather than minimum 510 mm) to provide additional safety margin and to ensure the footing has adequate rigidity. This also simplifies construction with a round number.
Verify Punching Shear with New Thickness
b₁ = b + d = 0.7 + 0.6 = 1.3 m
b₂ = b + d = 0.7 + 0.6 = 1.3 m
Ap = b₁ × b₂ = 1.3 × 1.3 = 1.69 m²
up = 2(b₁ + b₂) = 2(1.3 + 1.3) = 5.2 m
Vpd = Nd – σz × Ap
Vpd = 2500 – (400 × 1.69)
Vpd = 2500 – 676
Vpd = 1824 kN
Vpr = γ × fctd × up × d
Vpr = 1 × 1 × 5200 × 600
Vpr = 3,120,000 N = 3120 kN
Vpd = 1824 kN < Vpr = 3120 kN ✓
Punching shear capacity is adequate with 71% reserve capacity!
Verify Modified Bearing Capacity
fzm = fcd – 18H
fzm = 525 – (18 × 0.65)
fzm = 525 – 11.7
fzm = 513.3 kN/m²
Bearing capacity remains satisfied.
One-Way Shear Check (Beam Shear)
Cantilever projection = (B₂ – b) / 2 = (2.5 – 0.7) / 2 = 0.9 m
Shear at critical section:
Distance from edge = 0.9 – 0.6 = 0.3 m (but check at d from column)
Vds = σz × [(B₂ – b)/2 – 0] × B₁
Vds = 400 × [(2.5 – 0.7)/2] × 2.5
Vds = 400 × 0.9 × 2.5
Vds = 900 kN
Concrete shear capacity:
Vcr = 0.65 × fctd × B₁ × d
Vcr = 0.65 × 1 × 2500 × 600
Vcr = 975,000 N = 975 kN
Vds = 900 kN < Vcr = 975 kN ✓
One-way shear capacity is adequate. Footing thickness H is sufficient.
Calculate Bending Moment
Cantilever moment per unit width:
Mds = (σz / 2) × [(B₂ – b) / 2]² × B₁
Mds = (400 / 2) × [(2.5 – 0.7) / 2]² × 2.5
Mds = 200 × (0.9)² × 2.5
Mds = 200 × 0.81 × 2.5
Mds = 405 kNm
Alternative calculation:
Mds = (400 × 0.9 × 2.5 × 0.9/2) = 405 kNm ✓
The footing acts as a cantilever beam projecting from the column. The upward soil pressure creates bending at the column face, requiring tensile reinforcement at the bottom of the footing.
Calculate Lever Arm
a = d – √(d² – 2Mds / (0.85 × fcd × B₁))
a = 600 – √(600² – (2 × 405 × 10⁶) / (0.85 × 20 × 2500))
Note: fcd = 20 MPa for C30 concrete
But calculation uses fcd = 13 MPa (conservative)
a = 600 – √(360,000 – (810 × 10⁶) / (0.85 × 13 × 2500))
a = 600 – √(360,000 – (810 × 10⁶) / 27,625)
a = 600 – √(360,000 – 29,322)
a = 600 – √330,678
a = 600 – 575.05
a = 24.95 mm ≈ 25 mm
The small value of ‘a’ (25 mm) indicates the section is lightly stressed in bending, which is typical for properly proportioned footings where punching shear usually governs the thickness.
Calculate Required Steel Area
As = Mds / [fyd × (d – a/2)]
As = (405 × 10⁶) / [365 × (600 – 24.95/2)]
As = (405 × 10⁶) / [365 × (600 – 12.48)]
As = (405 × 10⁶) / [365 × 587.52]
As = (405 × 10⁶) / 214,445
As = 1888.58 mm²
Check minimum reinforcement:
As,min = 0.002 × B₁ × H
As,min = 0.002 × 2500 × 650
As,min = 3250 mm²
As,calculated = 1888.58 mm² < As,min = 3250 mm²
Use minimum reinforcement: As = 3250 mm²
Minimum reinforcement ensures adequate crack control, proper load distribution, and ductile behavior. It’s common for footings to be governed by minimum reinforcement rather than strength requirements.
Select Reinforcement Bars
Area of Ø16 bar = π × 16² / 4 = 201 mm²
Number of bars required:
n = As / Abar
n = 3250 / 201
n = 16.17
Round up to: n = 17 bars
Total area provided:
As,provided = 17 × 201 = 3417 mm²
Reinforcement is adequate with 5% excess.
Calculate Bar Spacing
Number of spaces = n – 1 = 17 – 1 = 16
Spacing = 2500 / 16 = 156.25 mm
Use: s = 156 mm
Check maximum spacing:
smax = min(3H, 400 mm)
smax = min(3 × 650, 400) = 400 mm
(Note: practical maximum often limited to 250mm)
Spacing is well within code limits.
17Ø16 @ 156 mm c/c (or Ø16/156)
Provide in BOTH directions (square footing)
Design Summary and Verification
| Design Check | Required | Provided | Status |
|---|---|---|---|
| Footing area | ≥ 4.76 m² | 6.25 m² (2.5×2.5) | ✓ (31% excess) |
| Soil pressure | ≤ 525 kN/m² | 400 kN/m² | ✓ (24% margin) |
| Punching shear | 1824 kN demand | 3120 kN capacity | ✓ (71% reserve) |
| One-way shear | 900 kN demand | 975 kN capacity | ✓ (8% reserve) |
| Bending moment | 405 kNm | Adequate with As | ✓ |
| Steel area | 3250 mm² (min) | 3417 mm² (17Ø16) | ✓ (5% excess) |
| Bar spacing | ≤ 250 mm | 156 mm | ✓ |
| Thickness | ≥ 510 mm (punching) | 650 mm | ✓ (27% excess) |
Design Iterations Summary
Trial 1: H = 450 mm
- Effective depth d = 400 mm
- Punching shear: Vpd = 2016 kN > Vpr = 1760 kN ✗
- Result: FAILED – Insufficient thickness
Trial 2: H = 650 mm (Final)
- Effective depth d = 600 mm
- Punching shear: Vpd = 1824 kN < Vpr = 3120 kN ✓
- One-way shear: Vds = 900 kN < Vcr = 975 kN ✓
- All checks satisfied ✓
- Result: ACCEPTABLE
Key Learning: Punching shear governs the footing thickness, not bending moment!
Critical Design Insights
- Punching shear governed: Initial thickness of 450mm was inadequate. Required increase to 650mm for punching shear capacity
- Minimum reinforcement controlled: Calculated flexural steel (1889 mm²) was less than minimum (3250 mm²), so minimum governed
- Square footing benefits: Equal reinforcement in both directions simplifies construction and provides uniform behavior
- Conservative thickness: Selected 650mm vs minimum required 510mm provides additional rigidity and safety
- Adequate margins: All final checks show comfortable reserve capacity (8% to 71%)
- Practical spacing: 156mm spacing provides good distribution and meets all code requirements
- Cantilever ratio: 900mm cantilever vs 650mm thickness = 1.38, within typical range of 1.2-1.5
FINAL CONSTRUCTION SPECIFICATION
FOOTING DIMENSIONS: 2500 × 2500 mm
FOOTING THICKNESS: H = 650 mm
EFFECTIVE DEPTH: d = 600 mm
BOTTOM REINFORCEMENT (BOTH WAYS): 17Ø16 @ 156 mm c/c
CONCRETE GRADE: C30 (fck = 30 MPa)
STEEL GRADE: S420 (fyk = 420 MPa)
CONCRETE COVER: 50 mm (bottom face)
COLUMN SIZE: 700 × 700 mm
DESIGN LOAD: Nd = 2500 kN
SOIL PRESSURE: σz = 400 kN/m²