ISOLATED SPREAD FOOTING DESIGN
Under Axial Load – Theoretical Background
Introduction to Spread Footings
Isolated spread footings are the most common foundation type for individual columns. They transfer column loads to the soil by spreading the load over a larger area, reducing the pressure on the soil to acceptable levels.
Design Principle: The footing must be designed to:
• Keep soil pressure within allowable limits
• Provide adequate structural strength against punching shear, one-way shear, and bending
• Ensure proper reinforcement for moment resistance
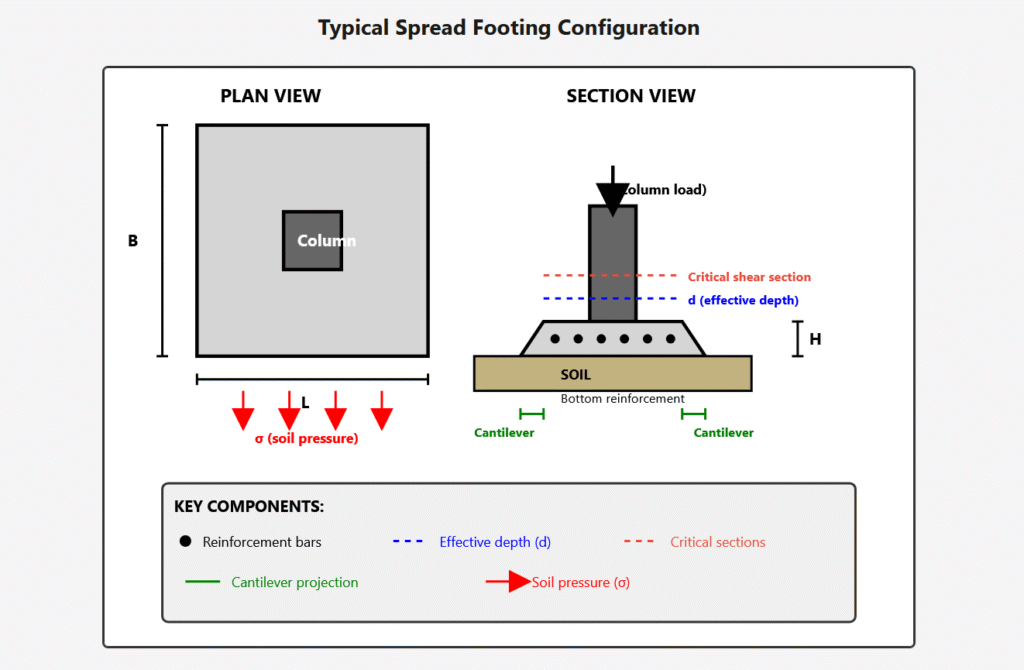
Typical Spread Footing Configuration
STEP-BY-STEP DESIGN PROCEDURE
Soil Bearing Capacity and Initial Sizing
For square footing: B = L
For rectangular footing: B and L are selected based on requirements
Preliminary sizing based on allowable soil pressure:
Areq = N / σallow
Where:
N = Column axial load (kN)
σallow = Allowable soil bearing pressure (kN/m²)
Areq = Required footing area (m²)
The footing area must be large enough so that the load distributed over the area does not exceed the soil’s bearing capacity. This is a serviceability check using unfactored loads.
Select Footing Dimensions
For square footing: B = L = √Areq
Round up to practical dimensions (multiples of 50mm or 100mm)
Example: If √Areq = 1.87 m → Select B = L = 2.0 m
Always round UP to ensure adequate area. Use standard increments for easier construction. Consider column dimensions when selecting footing size – adequate cantilever projection is needed.
Calculate Actual Soil Pressure
σactual = Nd / (B × L)
Where:
Nd = Factored column load (kN)
B × L = Actual footing area (m²)
Check: σactual ≤ σallow × γf
(where γf is load factor, typically 1.4-1.6)
For structural design (punching, shear, bending), use factored loads. For soil pressure verification, compare factored pressure against factored soil capacity or use unfactored loads with allowable soil pressure.
Determine Footing Thickness (H)
H ≥ 250 mm (code minimum)
H ≥ max(cantilever projection) / 4
Where cantilever = (B2 – b) / 2 or (L2 – l) / 2
Effective depth: d = H – cover – Ø/2
Typical cover for footings: 50-75 mm (soil contact)
For initial estimate: H ≈ L/10 to L/8 for economic design
The thickness must be verified against punching shear – this often governs the design!
Punching Shear Check (Critical Perimeter)
up = 2(b + d) + 2(l + d) = 2(b + l + 2d)
For square column (b = l):
up = 4(b + d)
Punching shear force:
Vpunch = Nd – σactual × Ap
Where Ap = area within critical perimeter = (b+d)(l+d)
Punching shear stress:
vp = Vpunch / (up × d)
Check: vp ≤ vp,allow = γ × fctd × up × d
(γ is a factor, typically around 1 for axial loads)
This is usually the most critical check. The column tends to “punch through” the footing. If this check fails, increase the footing thickness H (and thus effective depth d).
One-Way Shear Check (Beam Shear)
For each direction, shear force:
Vd = σactual × (B2 – b)/2 – d) × B1
Concrete shear capacity:
Vcr = 0.65 × fctd × B1 × d
Check: Vd < Vcr
If satisfied: Shear reinforcement is adequate
If not satisfied: Increase thickness or provide shear reinforcement
For properly proportioned footings, one-way shear is usually satisfied without additional reinforcement. Punching shear is more critical.
Calculate Bending Moments
Cantilever moment per meter width:
Md = (σactual/2) × ((B2 – b)/2)² × B1
Simplified for square footing with square column:
Md = (σactual/2) × ((B – b)/2)² × B (kNm)
This moment acts at the column face and must be resisted by
flexural reinforcement in the bottom of the footing.
The footing acts like a cantilever beam projecting from the column. Soil pressure creates upward force, causing bending. Bottom reinforcement resists tension.
Calculate Required Flexural Reinforcement
Lever arm: a = d – √(d² – 2Md/(0.85 × fcd × B))
Required steel area:
As = Md / (fyd × (d – a/2))
Minimum reinforcement:
As,min = 0.002 × B × H (mm²)
Use: As = max(As,calculated, As,min)
Minimum reinforcement ensures adequate crack control and distribution of stresses. Always check that calculated reinforcement exceeds minimum requirements!
Select Reinforcement Bar Size and Spacing
Number of bars per meter: n = As / Abar
Spacing: s = 1000 / n (mm)
Or: Select bar diameter and calculate spacing:
s = (1000 × Abar) / As
Where Abar = π × Ø² / 4
Maximum spacing limits:
s ≤ 3H or 400mm (whichever is smaller)
Practical Reinforcement Selection
- Common bar sizes: Ø10, Ø12, Ø14, Ø16, Ø20 mm
- Typical spacing: 100, 125, 150, 200, 250 mm
- Provide reinforcement in both directions for square footings
- For rectangular footings, more reinforcement in the long direction
- Always use at least minimum reinforcement
DESIGN SUMMARY CHECKLIST
Complete Design Verification Steps
- Soil Bearing: σactual ≤ σallow ✓
- Minimum Thickness: H ≥ 250 mm and H ≥ cantilever/4 ✓
- Punching Shear: vp ≤ vp,allow ✓
- One-Way Shear: Vd < Vcr ✓
- Bending Moment: Calculate Md at column face ✓
- Flexural Reinforcement: As ≥ As,min and adequate for Md ✓
- Bar Spacing: s ≤ 3H or 400mm ✓
- Development Length: Adequate anchorage beyond critical section ✓
Key Design Principles Summary
| Design Aspect | Formula/Criterion | Purpose |
|---|---|---|
| Area Sizing | A = N / σallow | Prevent soil failure |
| Minimum Thickness | H ≥ 250mm, H ≥ L/8 | Ensure rigidity and shear capacity |
| Punching Shear | Check at d/2 from column | Prevent punching failure |
| One-Way Shear | Check at d from column | Ensure beam shear capacity |
| Bending | M at column face | Size flexural reinforcement |
| Minimum Steel | 0.002 × B × H | Crack control and ductility |
| Maximum Spacing | s ≤ 3H or 400mm | Ensure proper load distribution |
Important Design Notes
- Load factors: Use factored loads (1.4 DL + 1.6 LL) for structural design calculations
- Soil pressure: Can check with service loads against allowable pressure, or factored loads against factored capacity
- Punching is critical: This usually governs footing thickness more than bending moment
- Effective depth: Remember d = H – cover – Ø/2. Use 50-75mm cover for footings in contact with soil
- Cantilever rule: H ≥ (projection)/4 ensures adequate stiffness
- Two-way action: Square footings need equal reinforcement in both directions
- Development length: Ensure bars extend far enough to develop full strength
- Construction joints: Consider pour sequences and proper load transfer
Ready for Practice Problems
Now that you understand the theoretical background and step-by-step procedure, you can apply these principles to actual design problems. The next section will provide worked examples demonstrating the complete design process.
Remember: Always follow the sequence: sizing → thickness → punching → shear → bending → reinforcement