Structural Engineering – Shear Design
Column Shear Reinforcement Design (Transverse Reinforcement)
Design of Stirrups/Ties for Rectangular Column
Problem Statement
For the rectangular column designed in the previous example (400 mm × 600 mm with 8Ø20 longitudinal reinforcement), calculate the required transverse reinforcement (stirrups/ties) to resist the design shear force.
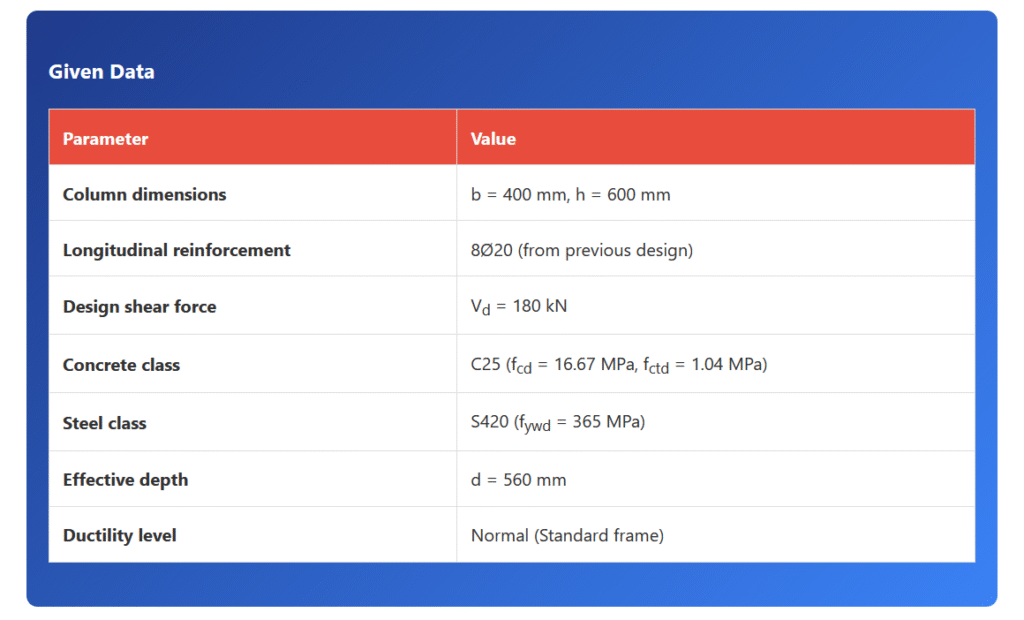
Given Data
| Parameter | Value |
|---|---|
| Column dimensions | b = 400 mm, h = 600 mm |
| Longitudinal reinforcement | 8Ø20 (from previous design) |
| Design shear force | Vd = 180 kN |
| Concrete class | C25 (fcd = 16.67 MPa, fctd = 1.04 MPa) |
| Steel class | S420 (fywd = 365 MPa) |
| Effective depth | d = 560 mm |
| Ductility level | Normal (Standard frame) |
THEORY – Shear Resistance in Columns
Maximum Shear Force Check
The column must satisfy the condition:
Vd ≤ 0.22 Ac fcd
Note: If this condition is NOT satisfied, dimensions must be increased.
If satisfied: Calculate the required shear reinforcement considering the cracking contribution of concrete.
Shear Resistance Components
Vd = Vc + Vs
Where:
Vc = Concrete contribution to shear resistance
Vs = Stirrup/tie contribution to shear resistance
Where:
Vc = Concrete contribution to shear resistance
Vs = Stirrup/tie contribution to shear resistance
For Normal Ductility Level Columns:
Concrete Contribution:
Vc = 0.8 Vcr (kN)
Vcr = Vd – Vc (kN)
Vcr = Vd – Vc (kN)
Stirrup Spacing:
s = (Asw fywd d) / Vs (mm)
Design Regions for Columns
CONFINEMENT ZONE (Near beam-column joints):
- Length = max(b/3, 8Ølong, 150 mm)
- Stricter spacing requirements
- s ≤ min(b/2, 12Ømin, 200 mm)
- Asw/sc ≥ 0.3 (fcd/fywd) b (minimum)
MIDDLE REGION:
- Less critical area
- s ≤ min(b/2, 12Ømin, 200 mm)
- Asw/so ≥ 0.3 (fcd/fywd) b
Important Note: For circular columns, use dn (diameter) instead of b (width). The section in brackets indicates this is the short side of the column.
SOLUTION – Step by Step Design
Step 1
Check Maximum Shear Force Capacity
Check: Vd ≤ 0.22 Ac fcd
Ac = b × h = 400 × 600 = 240,000 mm²
fcd = 16.67 MPa
0.22 Ac fcd = 0.22 × 240,000 × 16.67
= 879,648 N = 879.6 kN
Vd = 180 kN < 879.6 kN ✓
Ac = b × h = 400 × 600 = 240,000 mm²
fcd = 16.67 MPa
0.22 Ac fcd = 0.22 × 240,000 × 16.67
= 879,648 N = 879.6 kN
Vd = 180 kN < 879.6 kN ✓
Result: The column dimensions are adequate for shear! The shear force (180 kN) is only 20.5% of the maximum capacity (879.6 kN).
Step 2
Calculate Required Stirrup Area for Shear
Concrete contribution to shear resistance:
Vcr = Vd × 0.65 fctd b d [1 + 0.07 (Nd/Ac)]
For this example (no significant axial compression effect):
Vc = 0.8 × Vcr
Simplified calculation (conservative approach):
Vc ≈ 0.8 × 0.65 × 1.04 × 400 × 560
= 0.8 × 152,064 N = 121.7 kN
For this example (no significant axial compression effect):
Vc = 0.8 × Vcr
Simplified calculation (conservative approach):
Vc ≈ 0.8 × 0.65 × 1.04 × 400 × 560
= 0.8 × 152,064 N = 121.7 kN
Required stirrup contribution:
Vs = Vd – Vc
Vs = 180 – 121.7 = 58.3 kN
Vs = 180 – 121.7 = 58.3 kN
What does this mean?
The concrete alone can resist 121.7 kN of shear. We need stirrups to provide an additional 58.3 kN of shear resistance.
The concrete alone can resist 121.7 kN of shear. We need stirrups to provide an additional 58.3 kN of shear resistance.
Step 3
Calculate Required Stirrup Spacing
Let’s try Ø10 two-legged stirrups:
Area of Ø10 bar = π × 10²/4 = 78.5 mm²
Two-legged stirrup: Asw = 2 × 78.5 = 157 mm²
Required spacing from shear:
s = (Asw × fywd × d) / Vs
s = (157 × 365 × 560) / (58,300)
s = 32,095,600 / 58,300
s = 550 mm
Two-legged stirrup: Asw = 2 × 78.5 = 157 mm²
Required spacing from shear:
s = (Asw × fywd × d) / Vs
s = (157 × 365 × 560) / (58,300)
s = 32,095,600 / 58,300
s = 550 mm
Step 4
Apply Maximum Spacing Limits
Confinement Zone Requirements:
Length of confinement zone = max(b/3, 8Ølong, 150 mm)
= max(400/3, 8×20, 150)
= max(133, 160, 150)
= 160 mm from column end
Maximum spacing in confinement zone:
sc ≤ min(b/2, 12Ømin, 200 mm)
= min(400/2, 12×10, 200)
= min(200, 120, 200)
= 120 mm
= max(400/3, 8×20, 150)
= max(133, 160, 150)
= 160 mm from column end
Maximum spacing in confinement zone:
sc ≤ min(b/2, 12Ømin, 200 mm)
= min(400/2, 12×10, 200)
= min(200, 120, 200)
= 120 mm
Middle Region Requirements:
Maximum spacing in middle region:
so ≤ min(b/2, 12Ømin, 200 mm)
= 120 mm (same calculation)
so ≤ min(b/2, 12Ømin, 200 mm)
= 120 mm (same calculation)
Critical Decision:
Our calculated spacing from shear = 550 mm
Maximum allowed spacing = 120 mm
Therefore, spacing is controlled by maximum limits, not by shear requirements!
We will use s = 120 mm throughout.
Our calculated spacing from shear = 550 mm
Maximum allowed spacing = 120 mm
Therefore, spacing is controlled by maximum limits, not by shear requirements!
We will use s = 120 mm throughout.
Step 5
Check Minimum Reinforcement Requirement
Minimum stirrup area ratio:
Asw/s ≥ 0.3 (fcd/fywd) b
Asw/s ≥ 0.3 × (16.67/365) × 400
Asw/s ≥ 0.3 × 0.0457 × 400
Asw/s ≥ 5.48 mm²/mm
For our design (Ø10, two-legged, s = 120 mm):
Asw/s = 157/120 = 1.31 mm²/mm
Asw/s ≥ 0.3 (fcd/fywd) b
Asw/s ≥ 0.3 × (16.67/365) × 400
Asw/s ≥ 0.3 × 0.0457 × 400
Asw/s ≥ 5.48 mm²/mm
For our design (Ø10, two-legged, s = 120 mm):
Asw/s = 157/120 = 1.31 mm²/mm
Check: 1.31 < 5.48 ❌
Our spacing of 120 mm does NOT satisfy minimum reinforcement!
Solution: Use larger diameter stirrups or reduce spacing.
Our spacing of 120 mm does NOT satisfy minimum reinforcement!
Solution: Use larger diameter stirrups or reduce spacing.
Step 6
Revise Design – Try Ø12 Stirrups
Area of Ø12 bar = π × 12²/4 = 113 mm²
Two-legged stirrup: Asw = 2 × 113 = 226 mm²
Using s = 120 mm:
Asw/s = 226/120 = 1.88 mm²/mm
Still less than 5.48 ❌
Two-legged stirrup: Asw = 2 × 113 = 226 mm²
Using s = 120 mm:
Asw/s = 226/120 = 1.88 mm²/mm
Still less than 5.48 ❌
Try reducing spacing to s = 80 mm:
With Ø10 stirrups, s = 80 mm:
Asw/s = 157/80 = 1.96 mm²/mm
Still less than 5.48 ❌
Asw/s = 157/80 = 1.96 mm²/mm
Still less than 5.48 ❌
Try Ø12 stirrups with s = 40 mm:
Asw/s = 226/40 = 5.65 mm²/mm
5.65 > 5.48 ✓
5.65 > 5.48 ✓
Final design satisfies all requirements!
Use Ø12 two-legged stirrups @ 40 mm spacing
Use Ø12 two-legged stirrups @ 40 mm spacing
Step 7
Verify Shear Capacity with Final Design
Provided stirrup contribution:
Vs,provided = (Asw × fywd × d) / s
Vs,provided = (226 × 365 × 560) / 40
Vs,provided = 46,214,400 / 40
Vs,provided = 1,155,360 N = 1,155.4 kN
Total shear capacity:
VR = Vc + Vs,provided
VR = 121.7 + 1,155.4 = 1,277.1 kN
Vd = 180 kN < 1,277.1 kN ✓
Vs,provided = (Asw × fywd × d) / s
Vs,provided = (226 × 365 × 560) / 40
Vs,provided = 46,214,400 / 40
Vs,provided = 1,155,360 N = 1,155.4 kN
Total shear capacity:
VR = Vc + Vs,provided
VR = 121.7 + 1,155.4 = 1,277.1 kN
Vd = 180 kN < 1,277.1 kN ✓
Excellent! The design has significant reserve capacity (710% of required capacity).
Design Summary
Final Stirrup Arrangement
| Parameter | Value | Status |
|---|---|---|
| Design shear force (Vd) | 180 kN | Given |
| Maximum shear capacity | 879.6 kN | Adequate ✓ |
| Concrete contribution (Vc) | 121.7 kN | Calculated |
| Required stirrup contribution (Vs) | 58.3 kN | Calculated |
| Spacing from shear alone | 550 mm | Too large |
| Maximum allowed spacing | 120 mm | Code limit |
| Minimum Asw/s required | 5.48 mm²/mm | Code minimum |
| Confinement zone length | 160 mm from each end | Code requirement |
| Final stirrup design | Ø12 @ 40 mm | Satisfies all ✓ |
| Provided shear capacity | 1,277.1 kN | Very safe ✓ |
Key Design Insights
- Minimum reinforcement governs: Although shear requirements alone would allow 550mm spacing, code minimum reinforcement requires much tighter spacing (40mm).
- Over-designed for shear: The final design provides 1,277 kN capacity vs. 180 kN demand (710% safety factor).
- Practical considerations: Very tight stirrup spacing (40mm) may be difficult to construct. Consider using 4-legged stirrups or larger diameter with wider spacing.
- Alternative design: Could use Ø16 stirrups @ 80mm or Ø14 @ 60mm for better constructability.
- Confinement zones: Special attention needed at both ends (160mm from top and bottom) where beam-column joints occur.
Alternative Practical Design Options
Option 1: Four-legged stirrups
Use Ø10 four-legged stirrups @ 80mm
Asw = 4 × 78.5 = 314 mm²
Asw/s = 314/80 = 3.93 mm²/mm
Still < 5.48 ❌
Asw = 4 × 78.5 = 314 mm²
Asw/s = 314/80 = 3.93 mm²/mm
Still < 5.48 ❌
Option 2: Larger diameter with reasonable spacing
Use Ø16 two-legged stirrups @ 80mm
Asw = 2 × 201 = 402 mm²
Asw/s = 402/80 = 5.03 mm²/mm
Still < 5.48 ❌ (close though!)
Asw = 2 × 201 = 402 mm²
Asw/s = 402/80 = 5.03 mm²/mm
Still < 5.48 ❌ (close though!)
Option 3: Recommended practical solution
Use Ø14 two-legged stirrups @ 50mm
Asw = 2 × 154 = 308 mm²
Asw/s = 308/50 = 6.16 mm²/mm
6.16 > 5.48 ✓ (Better for construction!)
Asw = 2 × 154 = 308 mm²
Asw/s = 308/50 = 6.16 mm²/mm
6.16 > 5.48 ✓ (Better for construction!)
Construction Drawing Specification
COLUMN: 400 × 600 mm
Longitudinal Reinforcement: 8Ø20
Transverse Reinforcement (PRIMARY DESIGN): Ø12 @ 40 mm
Alternative (More Practical): Ø14 @ 50 mm
Confinement Zone: 160 mm from each end
Stirrup Configuration: Two-legged (rectangular ties)
Concrete: C25
Steel: S420
⚠️ Important Notes:
- This is a simplified design example. Actual design must consider all load combinations and detailing requirements.
- Very tight stirrup spacing may create concrete placement difficulties – coordinate with construction team.
- Local building codes (ACI 318, Eurocode 2, etc.) may have additional requirements.
- All designs must be reviewed and sealed by a licensed structural engineer.
