Structural Engineering – Circular Column Design
Circular Reinforced Concrete Column
Axial Load Capacity & Spiral Reinforcement Design
Problem Statement
Design a circular reinforced concrete column with specified reinforcement. Given the moment capacity and steel configuration, determine:
a) Maximum axial load (Nd) the column can support based on interaction diagrams
b) Spiral tie spacing for Ø8 mm bars based on calculated axial load
Material Properties
| Property | Value | Description |
|---|---|---|
| Concrete Class | C25 | fck = 25 MPa |
| Steel Class | S420 | fyk = 420 MPa |
| fcd | 16.67 MPa | Design concrete strength (25/1.5) |
| fyd | 365 MPa | Design steel strength (420/1.15) |
| Cover | 25 mm | Concrete cover to reinforcement |
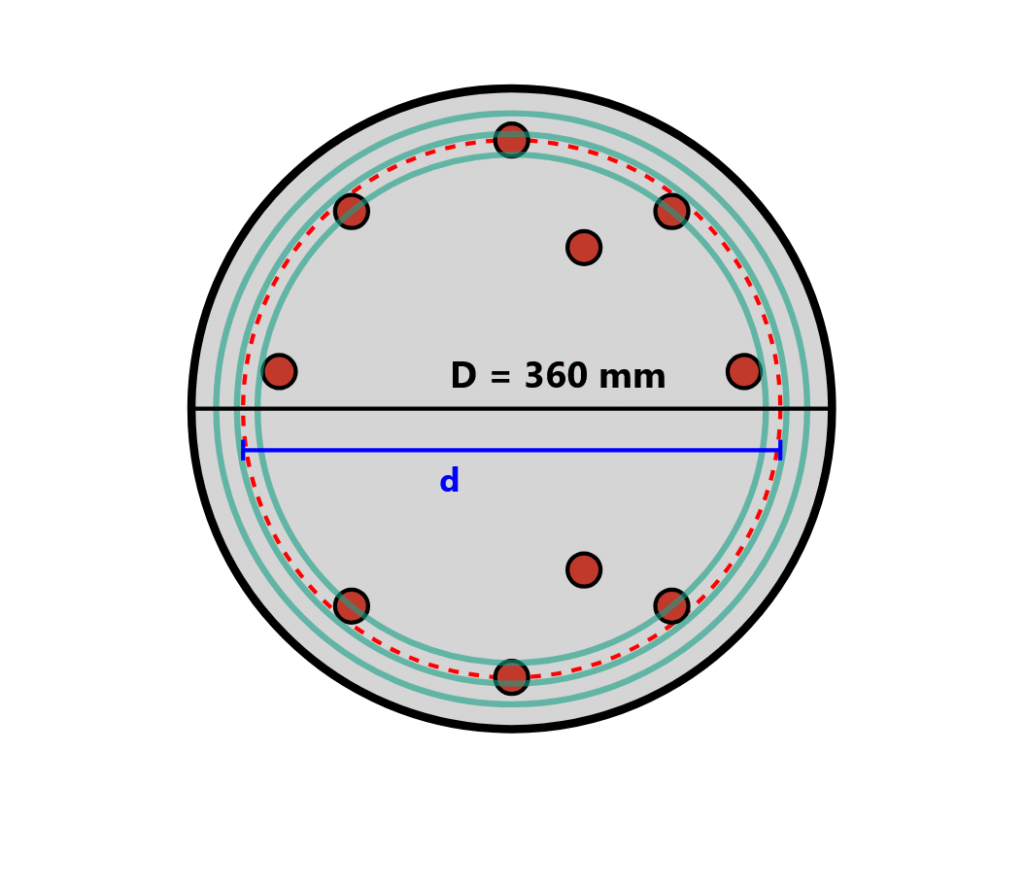
Column Geometry and Reinforcement
Circular Column Cross-Section
Column Specifications:
- Outer diameter (D): 360 mm
- Core diameter (dc): 310 mm (D – 2×cover)
- Concrete cover: 25 mm
- Longitudinal reinforcement: 10Ø16 bars uniformly distributed
- Transverse reinforcement: Ø8 spiral ties
Given Design Data
| Parameter | Value |
|---|---|
| Column diameter (D) | 360 mm |
| Core diameter (dc) | 310 mm |
| Longitudinal steel | 10Ø16 |
| Design moment (Md) | 108.96 kNm |
| Spiral bar size | Ø8 mm |
PART A: AXIAL LOAD CAPACITY DETERMINATION
Step 1
Calculate Gross Concrete Area
Ac = π D² / 4
Ac = π × 360² / 4
Ac = 3.14 × 129,600 / 4
Ac = 101,736 mm²
Ac = π × 360² / 4
Ac = 3.14 × 129,600 / 4
Ac = 101,736 mm²
Gross concrete area: This is the total cross-sectional area of the column including concrete and steel reinforcement.
Step 2
Calculate Core Area
Ack = π dc² / 4
Ack = π × 310² / 4
Ack = 3.14 × 96,100 / 4
Ack = 75,439 mm²
Ack = π × 310² / 4
Ack = 3.14 × 96,100 / 4
Ack = 75,439 mm²
Core area: The area within the centerline of the spiral reinforcement, critical for confinement calculations.
Step 3
Calculate Total Longitudinal Steel Area
Ast = 10 × (π × 16² / 4)
Ast = 10 × 201
Ast = 2,010 mm²
Ast = 10 × 201
Ast = 2,010 mm²
Total steel area: Combined cross-sectional area of all 10 longitudinal bars.
Step 4
Calculate Steel Ratio
ρs = Ast / Ac
ρs = 2,010 / 101,736
ρs = 0.0198 ≈ 0.02 = 2.0%
ρs = 2,010 / 101,736
ρs = 0.0198 ≈ 0.02 = 2.0%
Steel ratio check: ρs = 2.0% is within code limits (1.0% ≤ ρs ≤ 4.0%) ✓
Step 5
Calculate Steel Coefficient (ψ)
ψ = ρs × (fyd / fcd)
ψ = 0.02 × (365 / 16.67)
ψ = 0.02 × 21.9
ψ = 0.438 ≈ 0.44
ψ = 0.02 × (365 / 16.67)
ψ = 0.02 × 21.9
ψ = 0.438 ≈ 0.44
Steel coefficient: This dimensionless parameter represents the contribution of steel reinforcement relative to concrete and is used with interaction diagrams.
Step 6
Calculate Normalized Moment
μ = Md / (Ac × d × fcd)
Where d ≈ 0.8D = 0.8 × 360 = 288 mm (effective depth for circular section)
μ = 108.96 × 10⁶ / (101,736 × 288 × 16.67)
μ = 108,960,000 / 488,545,536
μ = 0.223 ≈ 0.22
Where d ≈ 0.8D = 0.8 × 360 = 288 mm (effective depth for circular section)
μ = 108.96 × 10⁶ / (101,736 × 288 × 16.67)
μ = 108,960,000 / 488,545,536
μ = 0.223 ≈ 0.22
Normalized moment: Dimensionless moment parameter for circular column interaction diagrams.
Step 7
Determine Normalized Axial Force from Interaction Diagram
From circular column interaction diagram:
With ψ = 0.44 and μ = 0.22
Read: ν ≈ 0.55
With ψ = 0.44 and μ = 0.22
Read: ν ≈ 0.55
Reading interaction diagrams: For circular columns with given steel coefficient (ψ) and moment (μ), we can determine the normalized axial force capacity (ν). This represents the interaction between moment and axial load.
Step 8
Calculate Maximum Axial Load Capacity
ν = Nd / (Ac × fcd)
Nd = ν × Ac × fcd
Nd = 0.55 × 101,736 × 16.67
Nd = 932,851 N
Nd ≈ 933 kN
Nd = ν × Ac × fcd
Nd = 0.55 × 101,736 × 16.67
Nd = 932,851 N
Nd ≈ 933 kN
ANSWER (Part a):
Maximum axial load capacity: Nd = 933 kN
(For Md = 108.96 kNm)
Maximum axial load capacity: Nd = 933 kN
(For Md = 108.96 kNm)
PART B: SPIRAL TIE SPACING DESIGN
Step 9
Check Axial Load Level
Check: Nd > 0.20 Ac fck
0.20 Ac fck = 0.20 × 101,736 × 25
= 508,680 N = 508.68 kN
Nd = 933 kN > 508.68 kN ✓
→ Spiral reinforcement design required
0.20 Ac fck = 0.20 × 101,736 × 25
= 508,680 N = 508.68 kN
Nd = 933 kN > 508.68 kN ✓
→ Spiral reinforcement design required
Design requirement: Since the axial load exceeds 20% of the column’s axial capacity, proper spiral reinforcement with adequate confinement is mandatory.
Step 10
Calculate Minimum Volumetric Spiral Ratio
ρsf ≥ max of:
Option 1: 0.45 × [(Ac/Ack) – 1] × (fck/fywk)
ρsf ≥ 0.45 × [(101,736/75,439) – 1] × (25/420)
ρsf ≥ 0.45 × [1.348 – 1] × 0.0595
ρsf ≥ 0.45 × 0.348 × 0.0595
ρsf ≥ 0.0093
Option 2: 0.12 × (fck/fywk)
ρsf ≥ 0.12 × (25/420)
ρsf ≥ 0.12 × 0.0595
ρsf ≥ 0.00714
Governing: ρsf = 0.0093
Option 1: 0.45 × [(Ac/Ack) – 1] × (fck/fywk)
ρsf ≥ 0.45 × [(101,736/75,439) – 1] × (25/420)
ρsf ≥ 0.45 × [1.348 – 1] × 0.0595
ρsf ≥ 0.45 × 0.348 × 0.0595
ρsf ≥ 0.0093
Option 2: 0.12 × (fck/fywk)
ρsf ≥ 0.12 × (25/420)
ρsf ≥ 0.12 × 0.0595
ρsf ≥ 0.00714
Governing: ρsf = 0.0093
Volumetric spiral ratio: This ratio ensures adequate confinement of the concrete core, which is critical for ductile behavior and enhanced compressive strength of the column.
Step 11
Calculate Spiral Bar Area
For Ø8 spiral:
Asp = π × 8² / 4
Asp = 3.14 × 64 / 4
Asp = 50.24 mm²
Asp = π × 8² / 4
Asp = 3.14 × 64 / 4
Asp = 50.24 mm²
Step 12
Calculate Required Spiral Spacing
ρsf = (4 × Asp) / (dc × s)
Solving for s:
s = (4 × Asp) / (dc × ρsf)
s = (4 × 50.24) / (310 × 0.0093)
s = 200.96 / 2.883
s = 69.7 mm ≈ 70 mm
Solving for s:
s = (4 × Asp) / (dc × ρsf)
s = (4 × 50.24) / (310 × 0.0093)
s = 200.96 / 2.883
s = 69.7 mm ≈ 70 mm
Step 13
Check Maximum Spacing Limits
Code maximum spacing limits for spirals:
s ≤ D/5 = 360/5 = 72 mm
s ≤ 80 mm (general limit)
Calculated: s = 70 mm
Check: 70 mm < 72 mm ✓
Check: 70 mm < 80 mm ✓
s ≤ D/5 = 360/5 = 72 mm
s ≤ 80 mm (general limit)
Calculated: s = 70 mm
Check: 70 mm < 72 mm ✓
Check: 70 mm < 80 mm ✓
Spacing is satisfactory! All code requirements are met.
Step 14
Select Final Spiral Spacing
Select standard spacing: s = 65 mm
(Rounded down to nearest 5 mm for practical construction)
(Rounded down to nearest 5 mm for practical construction)
ANSWER (Part b):
Spiral reinforcement: Ø8 @ 65 mm pitch
(8mm diameter bars at 65mm center-to-center spacing)
Spiral reinforcement: Ø8 @ 65 mm pitch
(8mm diameter bars at 65mm center-to-center spacing)
Complete Design Summary
| Design Parameter | Calculated Value | Final Design | Status |
|---|---|---|---|
| Column diameter | D = 360 mm | 360 mm | Given ✓ |
| Core diameter | dc = 310 mm | 310 mm | ✓ |
| Gross area | Ac = 101,736 mm² | – | ✓ |
| Core area | Ack = 75,439 mm² | – | ✓ |
| Longitudinal steel area | Ast = 2,010 mm² | 10Ø16 | Given ✓ |
| Steel ratio | ρs = 2.0% | Within limits | ✓ |
| Design moment | Md = 108.96 kNm | – | Given ✓ |
| Normalized moment | μ = 0.22 | – | ✓ |
| Steel coefficient | ψ = 0.44 | – | ✓ |
| Normalized axial force | ν = 0.55 | From diagram | ✓ |
| Axial capacity (Part a) | Nd = 933 kN | 933 kN | ✓ |
| Volumetric spiral ratio | ρsf = 0.0093 | Minimum required | ✓ |
| Spiral spacing calculated | s = 70 mm | – | ✓ |
| Spiral design (Part b) | s ≤ 72 mm | Ø8 @ 65 mm | ✓ |
Design Verification
Longitudinal Steel Verification:
- Steel ratio: 2.0% (within 1%-4% code limits) ✓
- Minimum bar diameter: Ø16 mm (adequate) ✓
- Number of bars: 10 (minimum 6 for circular columns) ✓
- Bar spacing: Uniform distribution around circumference ✓
Spiral Reinforcement Verification:
- Spiral diameter: Ø8 mm (minimum Ø6 mm) ✓
- Spacing: 65 mm (< 72 mm and < 80 mm limits) ✓
- Volumetric ratio: Meets both code equations ✓
- Confinement: Adequate for ductile behavior ✓
Capacity Checks:
- Axial load: 933 kN (with Md = 108.96 kNm) ✓
- Load level: > 20% Acfck (spiral required) ✓
- Interaction: Within column capacity envelope ✓
Key Design Insights
- Circular column advantages: Better confinement, improved ductility, uniform strength in all directions
- High steel ratio (2%): Provides significant moment capacity and enhanced axial load resistance
- Interaction design: The column can support 933 kN axial load when subjected to 108.96 kNm bending moment simultaneously
- Spiral confinement: 65mm spacing provides excellent core confinement, critical for seismic performance
- Practical construction: 10 bars allow for manageable spacing and ease of assembly
- Moment effect: Normalized moment μ = 0.22 indicates moderate bending, requiring consideration in interaction
- Spiral vs ties: Continuous spiral provides superior confinement compared to discrete rectangular ties
Final Construction Specification
CIRCULAR COLUMN: Ø360 mm
CORE DIAMETER: 310 mm
LONGITUDINAL REINFORCEMENT: 10Ø16
SPIRAL REINFORCEMENT: Ø8 @ 65 mm pitch
CONCRETE GRADE: C25 (fck = 25 MPa)
STEEL GRADE: S420 (fyk = 420 MPa)
CONCRETE COVER: 25 mm clear
DESIGN CAPACITY: Nd = 933 kN @ Md = 108.96 kNm
