Complete truss analysis using the Method of Joints with step-by-step solutions. Learn to calculate member forces, identify tension and compression members, and apply equilibrium equations at each joint. Features detailed free body diagrams, sign conventions, and practical design considerations for a symmetric truss structure.

TRUSS MEMBER FORCE CALCULATION

Statics, Civil Engineering, Engineering, How To / Leave a Comment
Truss Member Force Analysis – Method of Joints
Statics – Method of Joints Analysis

TRUSS MEMBER FORCE CALCULATION

Complete Analysis Using Method of Joints

METHODS FOR CALCULATING TRUSS MEMBER FORCES

A. Method of Joints – Analyzes equilibrium at each joint/node

B. Method of Sections (Ritter Method) – Analyzes equilibrium of cut sections

This tutorial focuses on the Method of Joints approach

METHOD OF JOINTS – Theory and Procedure

Fundamental Principles

  1. Start from the simplest joint: Begin analysis at a joint with the fewest unknowns (ideally 2 unknown forces)
  2. External forces affect joints: Support reactions, external loads (roof loads, etc.) act as forces at the joints, and forces are transmitted through members connecting to those joints
  3. Member force assumptions: When analyzing the joint where members are connected, if the sign of the member force is unknown, assume the member is in tension or compression. The result of the calculation determines the actual state:
    • Positive (+) result → Member is in TENSION (pulling away from joint)
    • Negative (-) result → Member is in COMPRESSION (pushing into joint)
    Members are therefore referred to as either tension or compression members.
  4. Equilibrium equations: At each joint in the analysis, all external forces and unknown member forces must satisfy equilibrium:
    • ΣFx = 0 (Sum of horizontal forces = 0)
    • ΣFy = 0 (Sum of vertical forces = 0)
    The method involves solving these equations for unknowns, then using those results to find member forces on the same member at other joints.

Sign Convention for Member Forces

T T

TENSION (+)

Member pulls away from joint

C C

COMPRESSION (-)

Member pushes into joint

EXAMPLE PROBLEM

Problem Statement

Calculate the member forces in the truss shown below using the Method of Joints.

Truss Structure and Loading

A F B G C H D E 6 kN 12 kN 12 kN 12 kN 6 kN Ay = 24 kN Ey = 24 kN 3 m 3 m 3 m 3 m 26.57°
Given Data:
  • Total applied loads: 4P = (6 + 12 + 12 + 12 + 6) = 48 kN
  • Support reactions (by symmetry): Ay = Ey = 48/2 = 24 kN
  • Panel width: 3 m each
  • Geometry: tan(α) = 2/3 → α = 26.57°

SOLUTION – Joint by Joint Analysis

Joint A

Analysis of Joint A

A Ay=24 kN 6 kN FAB FAF
ΣFx = 0:
FAB cos(26.57°) + FAF = 0
0.894 FAB + FAF = 0

ΣFy = 0:
Ay – 6 + FAB sin(26.57°) = 0
24 – 6 + 0.447 FAB = 0
18 + 0.447 FAB = 0
FAB = -40.27 kN

From ΣFx = 0:
0.894(-40.27) + FAF = 0
FAF = 36.0 kN
Joint A Results: FAB = -40.27 kN (COMPRESSION), FAF = +36.0 kN (TENSION)
Joint F

Analysis of Joint F

F FAF 36.0 kN FFG
ΣFx = 0:
-FAF + FFG = 0
-36.0 + FFG = 0
FFG = 36.0 kN

ΣFy = 0:
(Automatically satisfied, no vertical components)
Note: Since there are no vertical forces or inclined members at joint F, FFG must equal FAF for horizontal equilibrium.
Joint F Result: FFG = +36.0 kN (TENSION)
Joint B

Analysis of Joint B

B 12 kN FBA 40.27 kN FBC FBF
ΣFx = 0:
-FBA cos(26.57°) + FBC cos(26.57°) = 0
-(-40.27) × 0.894 + FBC × 0.894 = 0
36.0 + 0.894 FBC = 0
FBC = -40.27 kN

ΣFy = 0:
-12 + FBA sin(26.57°) + FBC sin(26.57°) – FBF = 0
-12 + (-40.27)(0.447) + (-40.27)(0.447) – FBF = 0
-12 – 18 – 18 – FBF = 0
FBF = -48 kN
Joint B Results: FBC = -40.27 kN (COMPRESSION), FBF = -48 kN (COMPRESSION)
Joint C

Analysis of Joint C (Peak)

C 12 kN FCB FCD FCG
By symmetry: FCD = FCB = -40.27 kN

ΣFy = 0:
-12 + FCB sin(26.57°) + FCD sin(26.57°) – FCG = 0
-12 + (-40.27)(0.447) + (-40.27)(0.447) – FCG = 0
-12 – 18 – 18 – FCG = 0
FCG = -48 kN
Note: Due to symmetry about the centerline, joints D, H, and E will have identical force patterns to joints B, F, and A respectively.
Joint C Results: FCD = -40.27 kN (COMPRESSION), FCG = -48 kN (COMPRESSION)

Completing the Analysis

Due to the symmetric loading and geometry, the remaining joints (D, H, E) have identical force distributions to their mirror counterparts (B, F, A):

  • Joint D mirrors Joint B
  • Joint H mirrors Joint F
  • Joint E mirrors Joint A

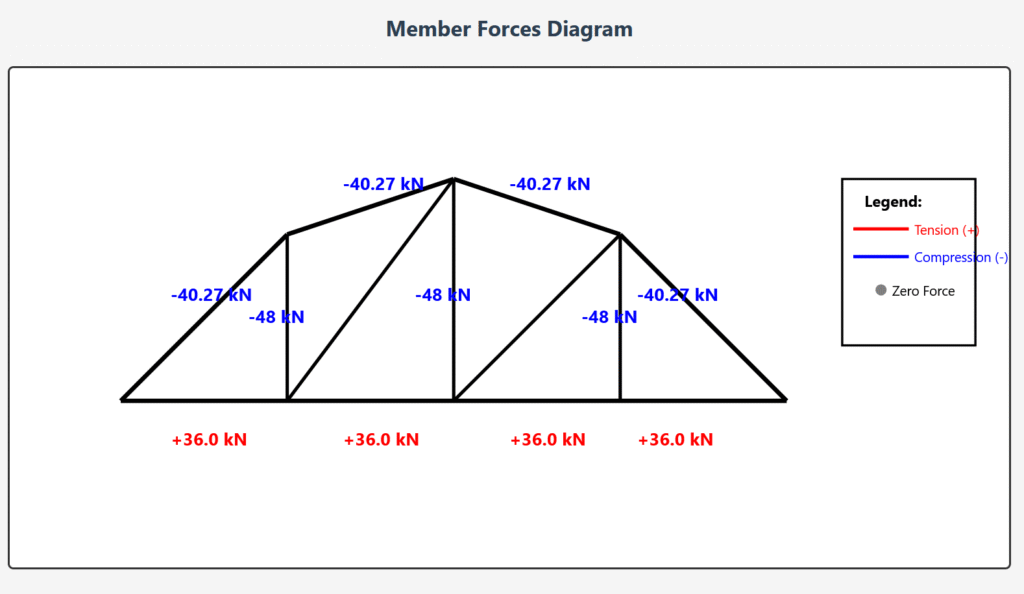
COMPLETE RESULTS SUMMARY

MemberForce (kN)TypeNotes
AB, DE-40.27CompressionInclined top chord members
BC, CD-40.27CompressionInclined top chord members
AF, EH+36.0TensionBottom chord members
FG, GH+36.0TensionBottom chord members
BF, DH-48.0CompressionVertical members
CG-48.0CompressionCenter vertical member
BG, DG0Zero-forceDiagonal members (zero-force members)

Member Forces Diagram

-40.27 kN -40.27 kN -40.27 kN -40.27 kN +36.0 kN +36.0 kN +36.0 kN +36.0 kN -48 kN -48 kN -48 kN Legend: Tension (+) Compression (-) Zero Force

SUMMARY OF MEMBER FORCES

COMPRESSION MEMBERS:

Top Chord: AB, BC, CD, DE = -40.27 kN

Verticals: BF, CG, DH = -48.0 kN

TENSION MEMBERS:

Bottom Chord: AF, FG, GH, HE = +36.0 kN

All equilibrium equations satisfied ✓

Key Observations and Learning Points

  1. Systematic Approach: Always start from joints with the fewest unknowns (typically 2)
  2. Sign Convention Consistency: Negative values indicate compression, positive indicate tension
  3. Symmetry Advantage: Recognize symmetric structures to reduce calculation effort
  4. Force Patterns: Top chords typically in compression, bottom chords in tension for downward loads
  5. Vertical Members: Usually in compression when loads act downward
  6. Equilibrium Check: Each joint must satisfy ΣFx = 0 and ΣFy = 0
  7. Member Design: Compression members need to be checked for buckling, tension members for yielding
Important Design Considerations:
  • Compression Members: Maximum force is 48 kN – must check buckling capacity based on length and cross-section
  • Tension Members: Maximum force is 36 kN – must check tensile yielding and net section capacity at connections
  • Connections: Joint design must accommodate maximum forces from all connecting members
  • Load Combinations: This analysis is for one load case – check multiple load combinations per code
  • Member Lengths: Diagonal members are longer (√(2²+3²) = 3.61 m) than horizontal members (3 m)

Must Read

Leave a Comment

Your email address will not be published. Required fields are marked *

Scroll to Top