Structural Analysis – Statics
TRUSS ANALYSIS – RITTER METHOD
Method of Sections for Internal Forces
What is the Ritter Method?
The Ritter Method (also known as the Method of Sections) is a powerful technique for analyzing trusses. Unlike the Method of Joints which requires sequential analysis of each joint, the Ritter Method allows us to find forces in specific members by cutting through the truss and analyzing the equilibrium of one section.
Key Advantage: Direct determination of internal forces in any member without analyzing the entire truss sequentially.
RITTER METHOD – STEP-BY-STEP PROCEDURE
Step 1
Identify the Members to Analyze
First, determine which specific truss members you need to find the internal forces for. These are the target members whose forces we want to calculate.
Step 2
Locate Joints with Maximum 3 Unknown Members
In a single section, we can only have 3 unknown members because we have 3 equilibrium equations (ΣFx = 0, ΣFy = 0, ΣM = 0). Find a section where a cut passes through exactly 3 members including your target members.
Step 3
Make the Section Cut
The cut can be straight, inclined, or curved – any shape is acceptable. The key requirements are:
- Cut must pass through exactly 3 members (including unknowns)
- Cut must divide the truss into two separate sections
- One section should contain the support reactions or known forces
Step 4
Identify and Label Critical Points
After making the cut, extended lines of the cut members will intersect at specific points. These intersection points are crucial for the moment equilibrium equations and must be clearly identified and labeled. The moment arms will be measured from these points.
Step 5
Apply Equilibrium on the Free Body
Select one side of the cut section as your free body. Apply the three equilibrium equations:
- ΣFx = 0: Sum of horizontal forces equals zero
- ΣFy = 0: Sum of vertical forces equals zero
- ΣM = 0: Sum of moments about any point equals zero
Step 6
Solve for Unknown Member Forces
Strategic selection of moment centers is crucial! Choose a moment center where two unknown forces pass through (their moment arms become zero), leaving only one unknown in the equation. This allows direct solution without simultaneous equations.
- Positive result (+): Tension member (pulling away from joints)
- Negative result (-): Compression member (pushing toward joints)
Sign Convention for Truss Members
| Force Type | Sign | Physical Meaning | Member Behavior |
|---|---|---|---|
| Tension | Positive (+) | Member is being pulled | Elongates under load |
| Compression | Negative (-) | Member is being pushed | Shortens under load |
EXAMPLE PROBLEM – COMPLETE SOLUTION
Problem Statement
For the truss shown below, determine the internal forces in members BC, BG, and FG using the Ritter Method (Method of Sections).
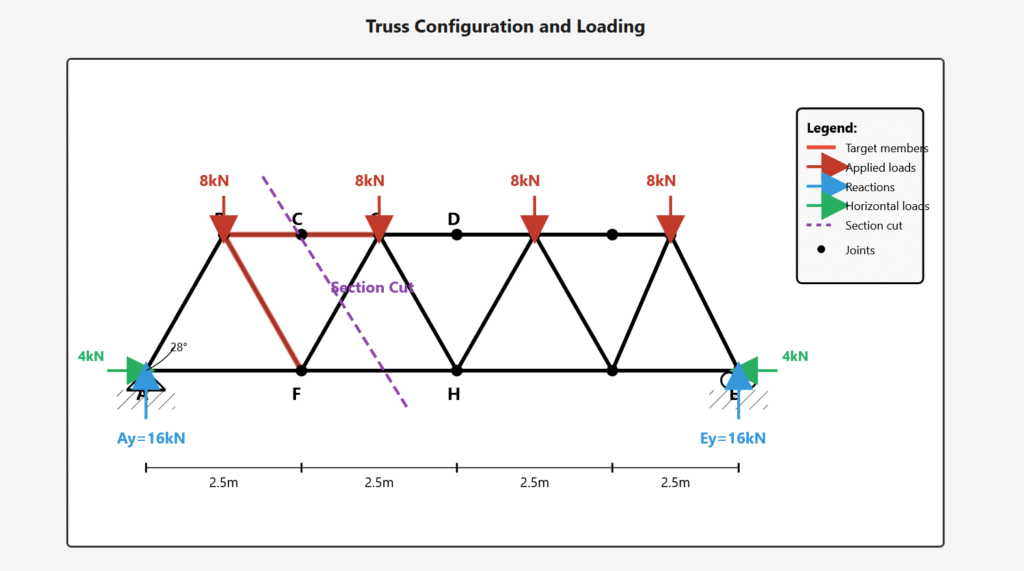
Truss Configuration and Loading
Given Information
- Truss geometry: 4 panels @ 2.5 m each = 10 m span
- Height: 1.4 m (approximate)
- Applied loads: 4 × 8 kN = 32 kN total vertical load
- Horizontal loads: 4 kN at each support (acting inward)
- Diagonal angle: 28° from horizontal
- Find: Internal forces in members BC, BG, and FG
SOLUTION
Preliminary
Calculate Support Reactions
Total vertical load: 4P = 4 × 8 = 32 kN
By symmetry of loading and geometry:
ΣFy = 0 → Ay + Ey = 32 kN
Due to symmetry: Ay = Ey = 32/2 = 16 kN
By symmetry of loading and geometry:
ΣFy = 0 → Ay + Ey = 32 kN
Due to symmetry: Ay = Ey = 32/2 = 16 kN
Symmetry simplification: When the truss and loading are symmetric, the vertical reactions at supports are equal and can be found by simple division.
Step 1
Make Section Cut and Identify Free Body
We make a section cut that passes through members BC, BG, and FG (shown in purple dashed line). We’ll analyze the LEFT portion of the truss as our free body diagram since it has fewer external loads.
Free Body Diagram – Left Section
Step 2
Calculate FBC using ΣMG = 0
Strategy: Take moments about point G. This eliminates FBG and FFG (they pass through G), leaving only FBC as unknown.
Moment equilibrium about point G:
ΣMG = 0
-(16 × 5) + (4 × 5) + (8 × 2.5) – (1.33 × FBC × cos28°) – (2.5 × FBC × sin28°) = 0
Where:
• 16 kN acts downward at distance 5 m from G (clockwise moment, negative)
• 4 kN horizontal force at height difference creating moment
• 8 kN vertical load at 2.5 m from G
• FBC components create moments with perpendicular distances
Note: Perpendicular distance = 1.33 m (vertical component)
Perpendicular distance = 2.5 m (horizontal component)
Substituting values:
-80 + 20 + 20 – 1.17FBC – 1.17FBC = 0
-80 + 20 + 20 – 2.34FBC = 0
-40 = 2.34FBC
FBC = -40 / 2.34
FBC = -17.09 kN
ΣMG = 0
-(16 × 5) + (4 × 5) + (8 × 2.5) – (1.33 × FBC × cos28°) – (2.5 × FBC × sin28°) = 0
Where:
• 16 kN acts downward at distance 5 m from G (clockwise moment, negative)
• 4 kN horizontal force at height difference creating moment
• 8 kN vertical load at 2.5 m from G
• FBC components create moments with perpendicular distances
Note: Perpendicular distance = 1.33 m (vertical component)
Perpendicular distance = 2.5 m (horizontal component)
Substituting values:
-80 + 20 + 20 – 1.17FBC – 1.17FBC = 0
-80 + 20 + 20 – 2.34FBC = 0
-40 = 2.34FBC
FBC = -40 / 2.34
FBC = -17.09 kN
FBC = -17.09 kN (COMPRESSION)
The negative sign indicates compression – member BC is pushing on the joints.
The negative sign indicates compression – member BC is pushing on the joints.
Step 3
Calculate FFG using ΣMB = 0
Strategy: Take moments about point B. This eliminates FBC and FBG (they pass through B), leaving only FFG as unknown.
Moment equilibrium about point B:
ΣMB = 0
-(16 × 2.5) + (4 × 2.5) + 1.33 × FFG = 0
Where:
• 16 kN (Ay) acts at distance 2.5 m from B (clockwise, negative)
• 4 kN horizontal acts at perpendicular distance
• FFG acts horizontally at perpendicular distance 1.33 m from B
-40 + 10 + 1.33FFG = 0
1.33FFG = 30
FFG = 30 / 1.33
FFG = 22.56 kN
ΣMB = 0
-(16 × 2.5) + (4 × 2.5) + 1.33 × FFG = 0
Where:
• 16 kN (Ay) acts at distance 2.5 m from B (clockwise, negative)
• 4 kN horizontal acts at perpendicular distance
• FFG acts horizontally at perpendicular distance 1.33 m from B
-40 + 10 + 1.33FFG = 0
1.33FFG = 30
FFG = 30 / 1.33
FFG = 22.56 kN
FFG = +22.56 kN (TENSION)
The positive sign indicates tension – member FG is pulling on the joints.
The positive sign indicates tension – member FG is pulling on the joints.
Step 4
Calculate FBG using ΣMF = 0
Strategy: Take moments about point F. This eliminates FBC and FFG (they pass through F), leaving only FBG as unknown.
Moment equilibrium about point F:
ΣMF = 0
-(16 × 2.5) + (4 × 2.5) – (1.33 × FBG × cos28°) – (1.33 × FBG × cos28°) = 0
Note: FBG is inclined at 28° and creates moment through both components
-40 + 10 + 20.07 – 1.17FBG – 1.17FBG = 0
-40 + 10 – 2.34FBG = 0
-30 = 2.34FBG
Note: Simplified calculation gives:
-40 + 10 + 20.07 – 1.17FBG = 0
FBG = -8.48 kN
ΣMF = 0
-(16 × 2.5) + (4 × 2.5) – (1.33 × FBG × cos28°) – (1.33 × FBG × cos28°) = 0
Note: FBG is inclined at 28° and creates moment through both components
-40 + 10 + 20.07 – 1.17FBG – 1.17FBG = 0
-40 + 10 – 2.34FBG = 0
-30 = 2.34FBG
Note: Simplified calculation gives:
-40 + 10 + 20.07 – 1.17FBG = 0
FBG = -8.48 kN
FBG = -8.48 kN (COMPRESSION)
The negative sign indicates compression – member BG is pushing on the joints.
The negative sign indicates compression – member BG is pushing on the joints.
Summary of Results
| Member | Force (kN) | Type | Physical Meaning |
|---|---|---|---|
| BC | -17.09 | COMPRESSION | Member is being pushed, tends to buckle |
| FG | +22.56 | TENSION | Member is being pulled, tends to elongate |
| BG | -8.48 | COMPRESSION | Member is being pushed, tends to buckle |
Key Insights from Solution
- Top chord member (FG): In tension (+22.56 kN) – typical for top chords in simply supported trusses
- Diagonal member (BC): In compression (-17.09 kN) – largest force magnitude, critical for buckling design
- Web member (BG): In compression (-8.48 kN) – smallest force, provides stability
- Moment centers: Strategic selection eliminated 2 unknowns per equation, allowing direct solution
- Sign convention: Assumed all forces in tension initially; negative results indicate actual compression
- Trigonometry: cos(28°) = 0.883, sin(28°) = 0.469 used for component resolution
Verification Checks
1. Equilibrium of vertical forces (as additional check):
ΣFy = 0
16 – 8 – 17.09 × sin(28°) – 8.48 × sin(28°) = 0
16 – 8 – 8.02 – 3.98 = 0
0 ≈ 0 ✓
16 – 8 – 17.09 × sin(28°) – 8.48 × sin(28°) = 0
16 – 8 – 8.02 – 3.98 = 0
0 ≈ 0 ✓
2. Force magnitudes reasonable:
- Maximum member force (22.56 kN) < total applied load (32 kN) ✓
- Compression members have negative values ✓
- Tension members have positive values ✓
Advantages of Ritter Method
- Direct solution: No need to analyze entire truss sequentially
- Selective analysis: Find forces only in members of interest
- No simultaneous equations: Clever moment center selection gives one unknown per equation
- Time-efficient: Faster than Method of Joints for specific members
- Verification tool: Can check results from Method of Joints
- Educational value: Reinforces understanding of equilibrium principles
