Roof truss statics, Load calculation, Support reactions, Tributary area analysis, Snow load calculation, Wind load formula, Roof covering load, Structure self-weight, Altitude-dependent loads, Geometric analysis, Sloped length calculation, Joint loads, Equilibrium verification, Moment equilibrium, Force equilibrium, Symmetric loading, Truss spacing, Roof slope angle, Panel analysis, Static equilibrium, Reaction forces, Load distribution, Dead loads, Live loads, Pythagorean theorem application, Trigonometry in statics

ROOF TRUSS ANALYSIS

Statics, Civil Engineering, Engineering, How To / Leave a Comment
Roof Truss Statics Problem
Statics – Worked Example

ROOF TRUSS ANALYSIS

Complete Load Calculation and Support Reaction Analysis

PROBLEM STATEMENT

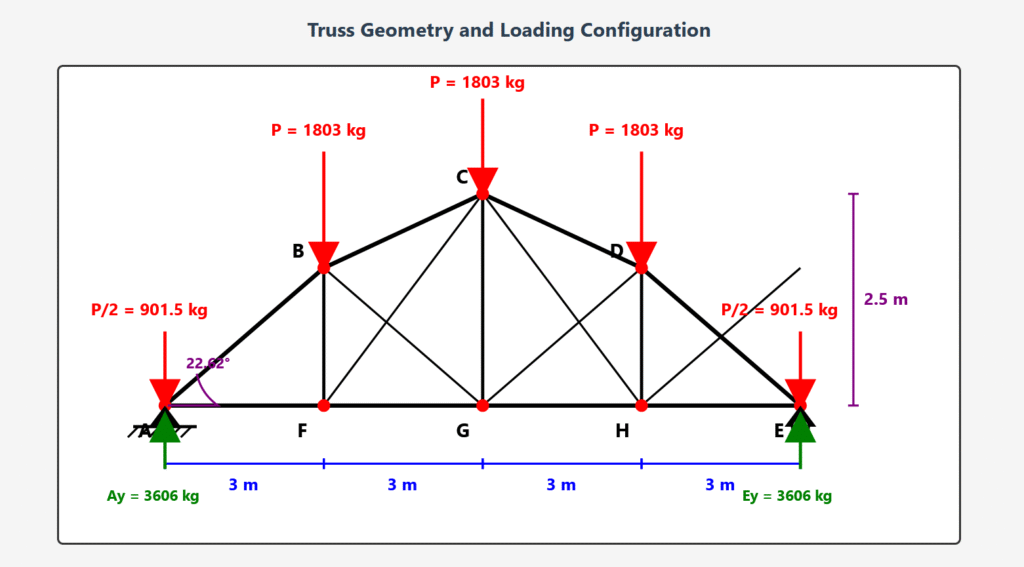
Calculate the joint loads and support reactions for a roof truss structure at the support points according to the given data:

  • Altitude: 900 m above sea level
  • Truss Spacing: 5.0 m
  • Structure Self-Weight: 10 kg/m²
  • Roof Covering Load: 12 kg/m²
  • Total Span: 12 m (divided into 4 panels of 3 m each)
  • Peak Height: 2.5 m above bottom chord

Truss Geometry and Loading Configuration

A F B G C H D E 3 m 3 m 3 m 3 m 2.5 m 22.62° P = 1803 kg P = 1803 kg P = 1803 kg P/2 = 901.5 kg P/2 = 901.5 kg Ay = 3606 kg Ey = 3606 kg

Given Data Summary

ParameterSymbolValue
AltitudeH900 m
Truss Spacing–5.0 m
Structure Self-WeightPMA10 kg/m²
Roof Covering LoadPÇÖ12 kg/m²
Panel Width–3.0 m
Total SpanL12 m
Peak HeightCG2.5 m
Half SpanGE6.0 m

SOLUTION – Complete Step by Step Analysis

Step 1

Calculate Roof Slope Angle

Using trigonometry for the roof slope:

tan(α) = CG / GE
tan(α) = 2.5 / 6.0
tan(α) = 0.4167
α = arctan(0.4167) = 22.62°
Roof Slope Angle: α = 22.62°
Understanding the geometry: The roof rises 2.5 m over a horizontal distance of 6.0 m (half the span), giving us the slope angle. This angle is crucial for calculating wind loads and determining the sloped length of the roof members.
Step 2

Calculate Sloped Length (CE)

Using Pythagorean theorem:

CE² = CG² + GE²
CE² = 2.5² + 6.0²
CE² = 6.25 + 36
CE² = 42.25
CE = √42.25 = 6.5 m
Total Sloped Length from Peak to Support: CE = 6.5 m
Verification: We can verify this using: CE = GE / cos(α) = 6.0 / cos(22.62°) = 6.0 / 0.923 = 6.5 m ✓
Step 3

Calculate Sloped Length per Panel (CD or DE)

Each panel sloped length:

CD = DE = CE / 2
CD = DE = 6.5 / 2
CD = DE = 3.25 m
Sloped Length per Panel: 3.25 m
Step 4

Calculate Tributary Areas

S1 – Sloped Area (for roof covering):

S1 = Sloped length × Truss spacing
S1 = 3.25 × 5.0
S1 = 16.25 m²
S2 – Horizontal Projection Area (for vertical loads):

S2 = Panel width × Truss spacing
S2 = 3.0 × 5.0
S2 = 15.0 m²
Tributary Areas: S1 = 16.25 m² (sloped), S2 = 15.0 m² (horizontal)
Key Concept:
  • S1 is used for loads applied perpendicular to the roof surface (roof covering, roofing materials)
  • S2 is used for loads acting vertically downward (snow, self-weight of structure)
Step 5

Calculate Snow Load (Pk)

Snow load formula (altitude-dependent):

Pk = 75 + 0.08(H – 1000) kg/m²

For H = 900 m (below 1000 m):
Pk = 75 + 0.08(900 – 1000)
Pk = 75 + 0.08(-100)
Pk = 75 – 8
Pk = 75 kg/m²
Snow Load Intensity: Pk = 75 kg/m²
Note: Since the altitude (900 m) is below the reference level of 1000 m, the snow load is actually reduced. At altitudes below 1000 m, snow loads decrease because lower elevations typically receive less snowfall.
Step 6

Calculate Total Snow Load at Joint (Wk)

Total snow load on one panel:

Wk = Pk × S2
Wk = 75 × 15.0
Wk = 1,125 kg
Snow Load at Each Interior Joint: Wk = 1,125 kg
Step 7

Calculate Wind Load (PR)

Wind load formula:

PR = 150 × (sin α)²
PR = 150 × (sin 22.62°)²
PR = 150 × (0.3846)²
PR = 150 × 0.1479
PR = 22.19 kg/m²
Wind Load Intensity: PR = 22.19 kg/m²
Step 8

Calculate Total Wind Load at Joint (WR)

Total wind load on one panel:

WR = PR × S2
WR = 22.19 × 15.0
WR = 332.85 kg ≈ 333 kg
Wind Load at Each Interior Joint: WR = 333 kg
Step 9

Calculate Roof Covering Load (WÇÖ)

Total roof covering load on one panel:

WÇÖ = PÇÖ × S1
WÇÖ = 12 × 16.25
WÇÖ = 195 kg
Roof Covering Load at Each Interior Joint: WÇÖ = 195 kg
Note: Roof covering load uses the sloped area (S1) because the material (tiles, shingles, etc.) is distributed along the actual slope surface.
Step 10

Calculate Structure Self-Weight (WMA)

Total self-weight on one panel:

WMA = PMA × S2
WMA = 10 × 15.0
WMA = 150 kg
Structure Self-Weight at Each Interior Joint: WMA = 150 kg
Step 11

Calculate Total Load at Interior Joints

Sum of all loads:

ΣP = Wk + WR + WÇÖ + WMA
ΣP = 1,125 + 333 + 195 + 150
ΣP = 1,803 kg
Total Load at Each Interior Joint (B, C, D): P = 1,803 kg
Load Distribution Breakdown:
  • Snow Load: 1,125 kg (62.4%)
  • Wind Load: 333 kg (18.5%)
  • Roof Covering: 195 kg (10.8%)
  • Self-Weight: 150 kg (8.3%)
  • Total: 1,803 kg (100%)
Step 12

Calculate Total Applied Load on Structure

Total load from all interior joints plus half loads at supports:

Total = (P/2 at A) + (P at B) + (P at C) + (P at D) + (P/2 at E)
Total = P/2 + P + P + P + P/2
Total = 4P

4P = 4 × 1,803
4P = 7,212 kg
Total Applied Load on Structure: 7,212 kg
Step 13

Calculate Support Reactions Using Symmetry

Due to symmetric loading and geometry:

Ay = Ey = Total Load / 2
Ay = Ey = 7,212 / 2
Ay = Ey = 3,606 kg
Support Reactions: Ay = Ey = 3,606 kg
Equilibrium Check (ΣFy = 0):
Ay + Ey – 4P = 0
3,606 + 3,606 – 7,212 = 0 ✓

The system is in equilibrium!
Step 14

Verify Using Moment Equilibrium

Taking moments about point A (ΣMA = 0):

Loads act at distances: 3m (B), 6m (C), 9m (D), 12m (E support)

ΣMA = -(1803×3) – (1803×6) – (1803×9) – (901.5×12) + 12Ey
0 = -5,409 – 10,818 – 16,227 – 10,818 + 12Ey
0 = -43,272 + 12Ey
12Ey = 43,272
Ey = 3,606 kg ✓
Moment Equilibrium Verified: Ey = 3,606 kg
Verification Complete:
  • Force equilibrium: ΣFy = 0 ✓
  • Moment equilibrium: ΣMA = 0 ✓
  • Reactions: Ay = Ey = 3,606 kg ✓
The solution satisfies all equilibrium conditions!

Complete Results Summary

DescriptionSymbolCalculated Value
Roof Slope Angleα22.62°
Total Sloped LengthCE6.5 m
Panel Sloped LengthCD = DE3.25 m
Sloped Tributary AreaS116.25 m²
Horizontal Tributary AreaS215.0 m²
Snow Load IntensityPk75 kg/m²
Wind Load IntensityPR22.19 kg/m²
Total Snow LoadWk1,125 kg
Total Wind LoadWR333 kg
Total Roof Covering LoadWÇÖ195 kg
Total Self-WeightWMA150 kg
Load at Interior Joints (B, C, D)P1,803 kg
Load at Support Joints (A, E)P/2901.5 kg
Total Applied Load4P7,212 kg
Support Reaction at AAy3,606 kg
Support Reaction at EEy3,606 kg

FINAL ANSWER

Joint Loads:

Interior Joints (B, C, D): P = 1,803 kg

Support Joints (A, E): P/2 = 901.5 kg

Support Reactions:

Ay = Ey = 3,606 kg

(Verified by both force and moment equilibrium)

Key Learning Points

  1. Geometric Analysis First: Always determine roof geometry (angle, sloped lengths) before load calculations
  2. Two Tributary Areas: Use sloped area for surface loads, horizontal area for vertical loads
  3. Altitude Effect: Snow loads decrease below 1000 m (by 0.08 kg/m² per meter) and increase above 1000 m
  4. Wind Load Formula: Proportional to sin²(α), meaning angle significantly affects wind pressure
  5. Load Superposition: Total load is the sum of all individual load components
  6. Half Loads at Supports: End joints receive half the load of interior joints due to tributary area
  7. Symmetry Advantage: Symmetric structures have equal reactions, simplifying analysis
  8. Equilibrium Verification: Always check both force and moment equilibrium to validate results
Important Design Considerations:
  • These are unfactored service loads. Apply load factors (typically 1.2 for dead, 1.6 for live) for ultimate limit state design
  • Analysis assumes loads applied only at joints (standard truss assumption)
  • Multiple load combinations must be checked per design codes
  • Wind and snow loads typically don’t act simultaneously at full values – check code requirements
  • Actual member forces in truss bars require method of joints or method of sections analysis

Must Read

Leave a Comment

Your email address will not be published. Required fields are marked *

Scroll to Top