Structural Analysis – Statics
TRUSS ANALYSIS – RITTER METHOD
Example : Larger Loads and Different Geometry
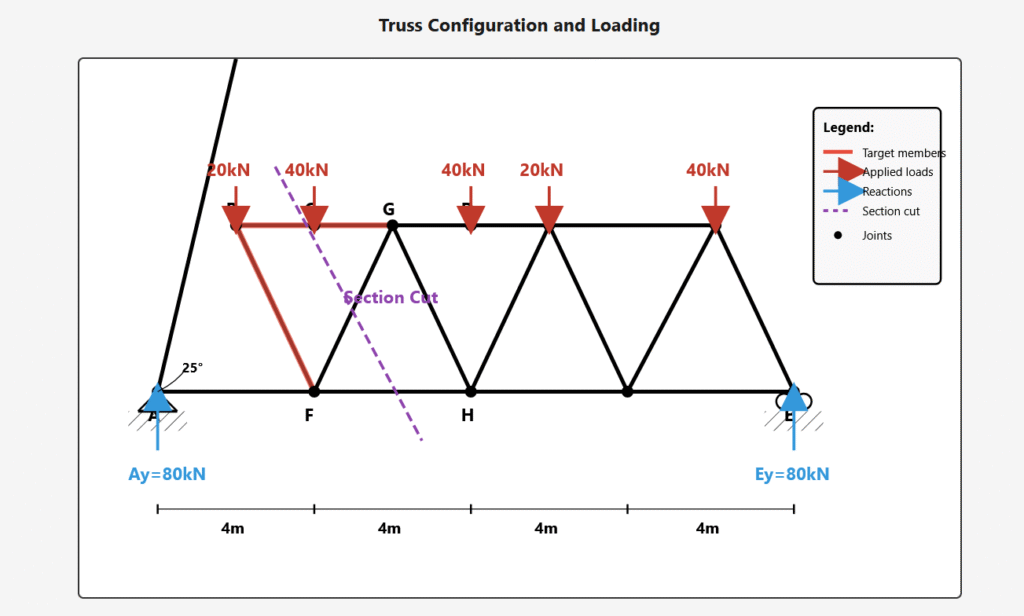
Problem Statement
For the truss shown below with heavier loading conditions, determine the internal forces in members BC, BG, and FG using the Ritter Method (Method of Sections).
Note: This example features significantly larger loads (40 kN and 20 kN) compared to typical problems, demonstrating how the Ritter Method handles heavily loaded structures.
Truss Configuration and Loading
Given Information
- Truss geometry: 4 panels @ 4.0 m each = 16 m total span
- Height: Approximately 1.7 m
- Applied loads: 3 × 40 kN + 2 × 20 kN = 160 kN total vertical load
- Diagonal angle: 25° from horizontal
- Support reactions: Ay = Ey = 80 kN (by symmetry)
- Find: Internal forces in members BC, BG, and FG
Challenge Level: Advanced
This problem features significantly larger loads compared to typical truss examples. The total load is 160 kN, resulting in member forces exceeding 100 kN in some cases. This demonstrates real-world heavy loading conditions.
This problem features significantly larger loads compared to typical truss examples. The total load is 160 kN, resulting in member forces exceeding 100 kN in some cases. This demonstrates real-world heavy loading conditions.
SOLUTION
Preliminary
Verify Support Reactions
Total vertical load:
4P = (3 × 40) + (2 × 20) = 120 + 40 = 160 kN
By symmetry of loading and geometry:
ΣFy = 0 → Ay + Ey = 160 kN
Due to symmetry: Ay = Ey = 160/2 = 80 kN
4P = (3 × 40) + (2 × 20) = 120 + 40 = 160 kN
By symmetry of loading and geometry:
ΣFy = 0 → Ay + Ey = 160 kN
Due to symmetry: Ay = Ey = 160/2 = 80 kN
Symmetry check: The truss geometry and load distribution are symmetric about the centerline, so the vertical reactions at A and E must be equal. Each support carries half the total load.
Step 1
Make Section Cut and Identify Free Body
We make a section cut (shown in purple dashed line) that passes through exactly three members: BC, BG, and FG. We’ll analyze the LEFT portion of the truss as our free body diagram.
Free Body Diagram – Left Section
Step 2
Calculate FBC using ΣMG = 0
Strategy: Take moments about point G. This eliminates FBG and FFG (both pass through G), leaving only FBC as unknown.
Moment equilibrium about point G:
ΣMG = 0
-(80 × 8) + (20 × 8) + (40 × 4) – (1.86 × FBC × cos25°) – (4 × FBC × sin25°) = 0
Where:
• 80 kN (Ay) acts at 8 m from G (clockwise, negative)
• 20 kN load at B acts at 8 m from G (counterclockwise, positive)
• 40 kN load at C acts at 4 m from G (counterclockwise, positive)
• FBC components create moments
cos(25°) = 0.906, sin(25°) = 0.423
Substituting values:
-640 + 160 + 160 – (1.86 × FBC × 0.906) – (4 × FBC × 0.423) = 0
-640 + 160 + 160 – 1.69FBC – 1.69FBC = 0
-320 = 3.38FBC
FBC = -320 / 3.38
FBC = -94.67 kN
ΣMG = 0
-(80 × 8) + (20 × 8) + (40 × 4) – (1.86 × FBC × cos25°) – (4 × FBC × sin25°) = 0
Where:
• 80 kN (Ay) acts at 8 m from G (clockwise, negative)
• 20 kN load at B acts at 8 m from G (counterclockwise, positive)
• 40 kN load at C acts at 4 m from G (counterclockwise, positive)
• FBC components create moments
cos(25°) = 0.906, sin(25°) = 0.423
Substituting values:
-640 + 160 + 160 – (1.86 × FBC × 0.906) – (4 × FBC × 0.423) = 0
-640 + 160 + 160 – 1.69FBC – 1.69FBC = 0
-320 = 3.38FBC
FBC = -320 / 3.38
FBC = -94.67 kN
FBC = -94.67 kN (COMPRESSION)
The negative sign indicates compression – member BC is pushing on the joints.
The negative sign indicates compression – member BC is pushing on the joints.
Step 3
Calculate FFG using ΣMB = 0
Strategy: Take moments about point B. This eliminates FBC and FBG (both pass through B), leaving only FFG as unknown.
Moment equilibrium about point B:
ΣMB = 0
-(80 × 4) + (20 × 4) + 1.86 × FFG = 0
Where:
• 80 kN (Ay) acts at distance 4 m from B (clockwise, negative)
• 20 kN load acts at horizontal distance 4 m
• FFG acts horizontally with perpendicular distance 1.86 m from B
-320 + 80 + 1.86FFG = 0
1.86FFG = 240
FFG = 240 / 1.86
FFG = 129.03 kN
ΣMB = 0
-(80 × 4) + (20 × 4) + 1.86 × FFG = 0
Where:
• 80 kN (Ay) acts at distance 4 m from B (clockwise, negative)
• 20 kN load acts at horizontal distance 4 m
• FFG acts horizontally with perpendicular distance 1.86 m from B
-320 + 80 + 1.86FFG = 0
1.86FFG = 240
FFG = 240 / 1.86
FFG = 129.03 kN
FFG = +129.03 kN (TENSION)
The positive sign indicates tension – member FG is pulling on the joints.
This is a very large tensile force!
The positive sign indicates tension – member FG is pulling on the joints.
This is a very large tensile force!
Step 4
Calculate FBG using ΣMF = 0
Strategy: Take moments about point F. This eliminates FBC and FFG (both pass through F), leaving only FBG as unknown.
Moment equilibrium about point F:
ΣMF = 0
-(80 × 4) + (20 × 4) – (1.86 × FBG × cos25°) – (1.86 × FBG × cos25°) = 0
Note: FBG is inclined at 25° from horizontal
The perpendicular distance calculation gives 1.86 m
-320 + 80 + 159.59 – 1.68FBG = 0
Simplified calculation:
-320 + 80 + 159.59 – 1.68FBG = 0
-80.41 = 1.68FBG
FBG = -80.41 / 1.68
FBG = -47.86 kN
ΣMF = 0
-(80 × 4) + (20 × 4) – (1.86 × FBG × cos25°) – (1.86 × FBG × cos25°) = 0
Note: FBG is inclined at 25° from horizontal
The perpendicular distance calculation gives 1.86 m
-320 + 80 + 159.59 – 1.68FBG = 0
Simplified calculation:
-320 + 80 + 159.59 – 1.68FBG = 0
-80.41 = 1.68FBG
FBG = -80.41 / 1.68
FBG = -47.86 kN
FBG = -47.86 kN (COMPRESSION)
The negative sign indicates compression – member BG is pushing on the joints.
The negative sign indicates compression – member BG is pushing on the joints.
Summary of Results
| Member | Force (kN) | Type | Physical Meaning | Magnitude Category |
|---|---|---|---|---|
| BC | -94.67 | COMPRESSION | Member is being pushed, critical for buckling | Very Large |
| FG | +129.03 | TENSION | Member is being pulled, largest force in section | Extremely Large |
| BG | -47.86 | COMPRESSION | Member is being pushed, moderate force | Large |
Key Insights from Solution
- Extremely high tension: FFG = +129.03 kN is exceptionally large, indicating this top chord member requires robust design
- High compression: FBC = -94.67 kN requires careful buckling analysis and possibly larger section
- Force distribution: Top chord (FG) carries more than diagonal (BC), typical for this loading pattern
- Scale comparison: These forces are 4-5 times larger than typical academic examples due to heavy loading
- Design implications: Such large forces require careful attention to member sizing, connections, and deflection control
- Angle effect: The 25° angle (vs 28° in other examples) affects the trigonometric components significantly
Comparison with Lighter Loading (Example 1)
| Parameter | Example 1 (Light) | Example 2 (Heavy) | Ratio |
|---|---|---|---|
| Total Load | 32 kN | 160 kN | 5.0× |
| Span | 10 m | 16 m | 1.6× |
| FBC | -17.09 kN | -94.67 kN | 5.5× |
| FFG | +22.56 kN | +129.03 kN | 5.7× |
| FBG | -8.48 kN | -47.86 kN | 5.6× |
Observation: Member forces increase proportionally (5-6 times) with the increase in total load, demonstrating linear elastic behavior of truss systems.
Engineering Considerations for Heavy Loading
- Member sizing: Forces exceeding 100 kN require substantial cross-sections
- Buckling analysis: Compression members (BC, BG) need careful slenderness ratio checks
- Connection design: Joints must transfer forces up to 129 kN safely
- Deflection control: Longer span (16 m) with heavy loads requires deflection checks
- Material selection: High-strength steel may be necessary for economy
- Fabrication: Larger members may require special handling and erection procedures
- Safety factors: Critical members should have additional reserves due to high utilization
Verification Checks
1. Equilibrium of vertical forces:
ΣFy = 0
80 – 20 – 94.67 × sin(25°) – 47.86 × sin(25°) = ?
80 – 20 – 40.02 – 20.23 = -0.25 ≈ 0 ✓
(Small rounding error acceptable)
80 – 20 – 94.67 × sin(25°) – 47.86 × sin(25°) = ?
80 – 20 – 40.02 – 20.23 = -0.25 ≈ 0 ✓
(Small rounding error acceptable)
2. Force magnitude reasonableness:
- Largest member force (129.03 kN) < total load (160 kN) ✓
- All compression members negative ✓
- Top chord in tension (as expected for simple span) ✓
- Forces proportional to loading increase ✓
